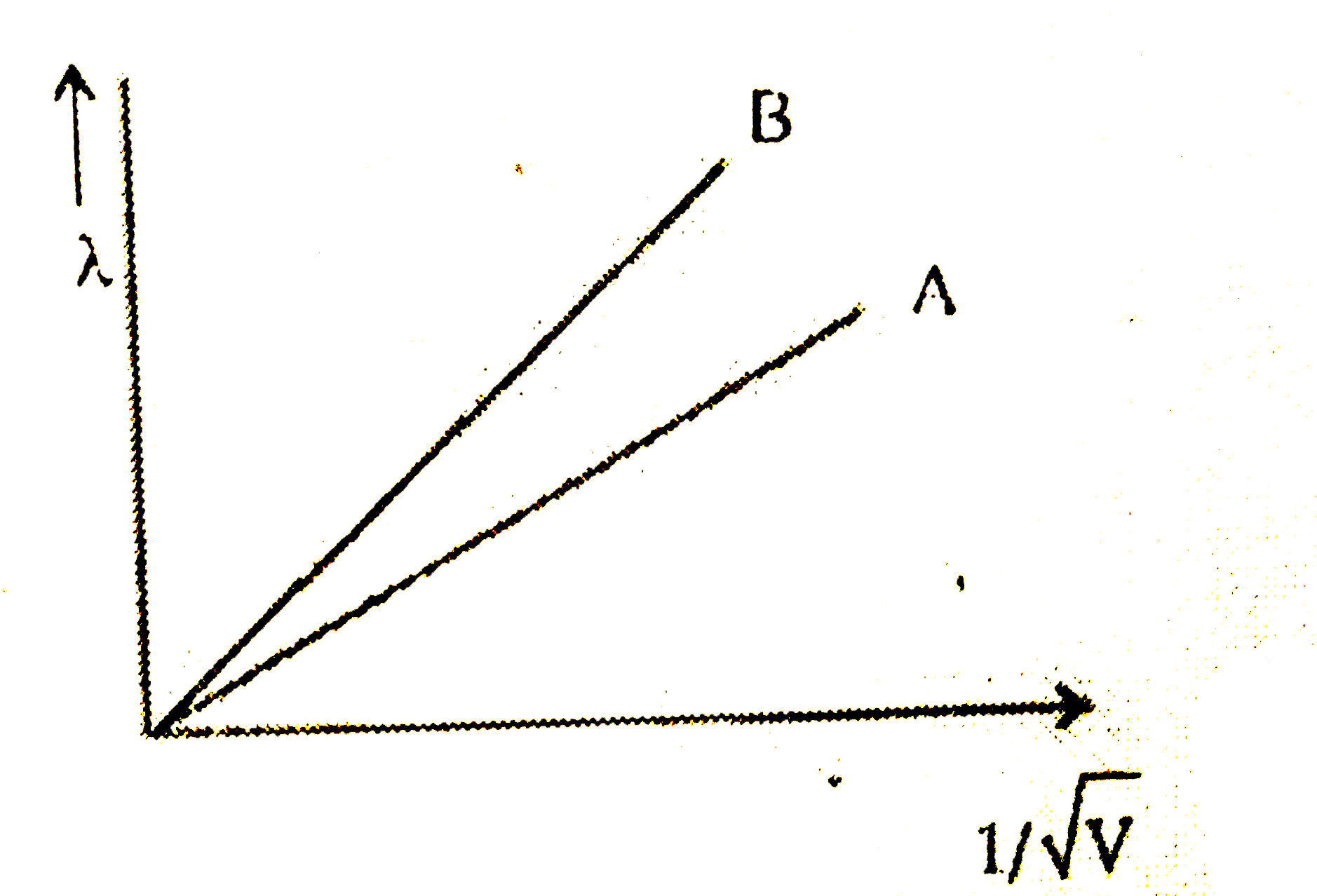
Plot a graph showing variation of de-broglie wavelength λ versus 1/√V, where V is accelerating potential for two particle A and P carrying same charge but of masses m1andm2(m1>m2). Which one of the two represents a particle of smaller mass and why?
To solve the problem, we need to analyze the relationship between the de Broglie wavelength (λ) and the accelerating potential (V) for two particles A and B with different masses but the same charge. Let's go through the steps to derive the relationship and plot the graph.
Step 1: Write the formula for de Broglie wavelength
The de Broglie wavelength (λ) of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
Step 2: Relate momentum to mass and velocity
The momentum p can also be expressed in terms of mass (m) and velocity (v):
p=mv
Step 3: Express velocity in terms of accelerating potential
For a charged particle accelerated through a potential V, the kinetic energy gained by the particle is equal to the work done on it by the electric field. Thus, we have:
12mv2=qV
where q is the charge of the particle. Rearranging this gives:
v=√2qVm
Step 4: Substitute velocity into the de Broglie wavelength formula
Now, substituting the expression for v into the de Broglie wavelength formula, we have:
λ=hmv=hm√2qVm=h√m√2qV
Step 5: Rearranging the equation
Rearranging the equation gives:
λ∝√m√V
This implies:
λ∝√m⋅1√V
Step 6: Plotting the graph
Now, if we plot the graph of λ versus 1√V, we can see that:
- For particle A with mass m1: λA∝√m1⋅1√V
- For particle B with mass m2: λB∝√m2⋅1√V
Since m1>m2, it follows that:
√m1<√m2
This means that the slope of the line for particle B (smaller mass) will be greater than that for particle A (larger mass).
Conclusion
The graph will show that the line corresponding to particle B (smaller mass m2) will have a steeper slope compared to that of particle A (larger mass m1). Thus, the particle with the smaller mass is represented by the line with the greater slope.
The de Broglie wavelength (λ) of a particle is given by the formula:
The momentum p can also be expressed in terms of mass (m) and velocity (v):
For a charged particle accelerated through a potential V, the kinetic energy gained by the particle is equal to the work done on it by the electric field. Thus, we have:
Now, substituting the expression for v into the de Broglie wavelength formula, we have:
Rearranging the equation gives:
Now, if we plot the graph of λ versus 1√V, we can see that:
- For particle B with mass m2: λB∝√m2⋅1√V
The graph will show that the line corresponding to particle B (smaller mass m2) will have a steeper slope compared to that of particle A (larger mass m1). Thus, the particle with the smaller mass is represented by the line with the greater slope.
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:Section -C
Explore 7 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:Section-E
Explore 17 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:Section -A
Explore 14 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.

View SolutionTwo lines, A and B, in the plot given below show the variation of de-Broglie wavelength, λ versus 1/√V, where V is the accelerating potential difference, for two particles carrying the same charge. Which one of two represents a particle of smaller mass?
View Solution
Knowledge Check
Two particles A1andA2 of masses m1,m2(m1>m2) have the same de-broglie wavelength. Then
Atheir momenta are the same.Btheir energies are the same.Cmomentum of A1 is less than the momentum of A2.Denergy of A1 is more than the energy of A2.

The two lines A and B in fig. shows the plot of de- Broglie wavelength (λ) as a function of 1√V(V is the accelerating potential) for the particles having the same charge. Which of the two represents the particle of heavier mass?
View SolutionPlot a graph showing variation of a de Broglie wavelength (λ) associated with a charged particle of mass m, verses 1/√V, where V is the potential difference thrugh which the particle is accelerated.
View SolutionDraw a graph showing the variation of de Broglie wavelength of a particle of charge q and mass m with accelerating potential. Proton and deuteron have the same de Broglie wavelengths. Explain which has more kinetic energy.
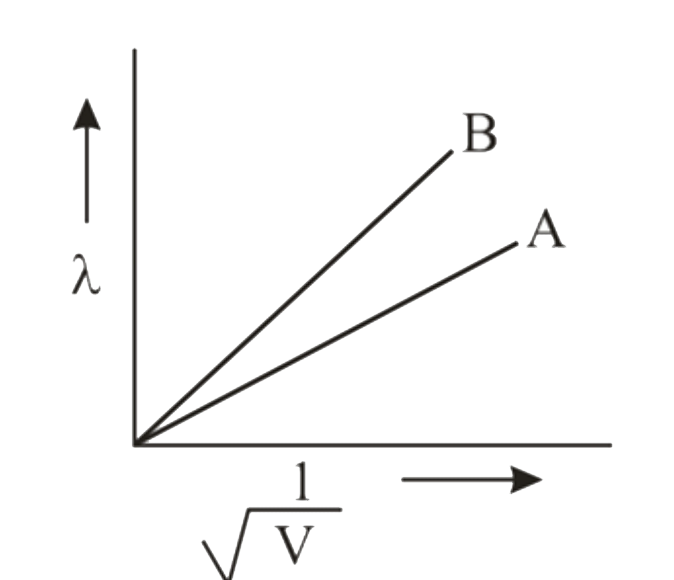
View Solutionde Broglie wavelengths of two particles A and B are plotted against (1√V) , where V is the potential on the particles. Which of the following relation is correct about the mass of the particles ?
View SolutionTwo particles A1andA2 of masses m1,m2(m1>m2) have the same de-broglie wavelength. Then
View SolutionThe de-Broglie wavelength of an α−particles at a voltage V is
(Given that α− particle has 2 units positive charge and 4 units mass )
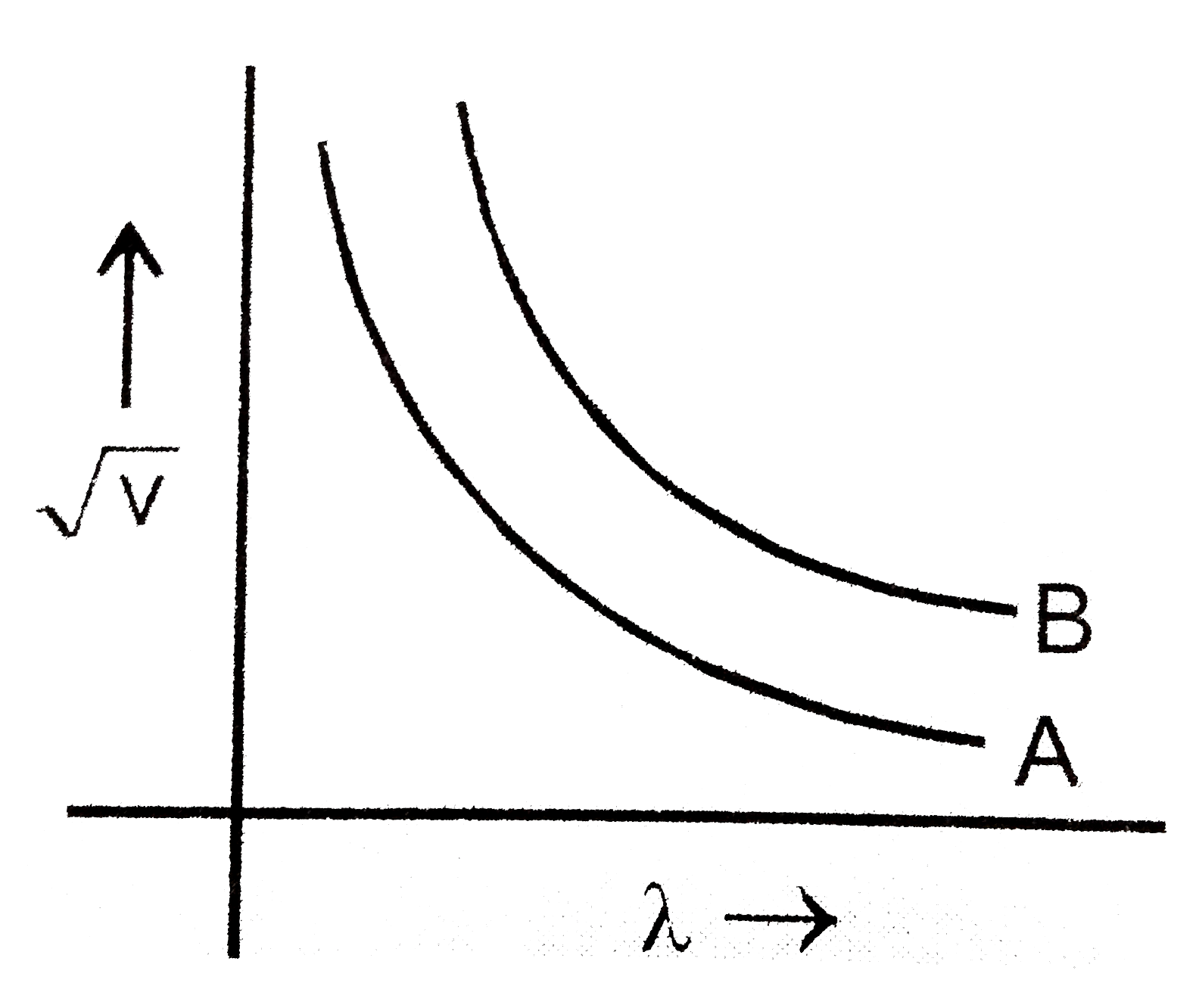
View SolutionFor two particles A and B, curves are plotted √V against de-Broglie wavelengths, where V is the potential on the particles. Which of the following relation is correct about the mass of particles?
View Solution

