A parallel plate capacitor of capacitane C is charged to a potential V. It is then connected to another uncharged capacitor with the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor.
To solve the problem step by step, let's analyze the situation involving the capacitors.
Step 1: Calculate the initial energy stored in the charged capacitor.
The energy stored in a capacitor is given by the formula:
U1=Q22C
where Q is the charge on the capacitor and C is the capacitance.
Since the capacitor is charged to a potential V, we can express the charge Q in terms of V and C:
Q=CV
Substituting this into the energy formula, we get:
U1=(CV)22C=CV22
Step 2: Analyze the system after connecting the uncharged capacitor.
When the charged capacitor is connected to an uncharged capacitor of the same capacitance C, the total capacitance of the system becomes:
Ctotal=C+C=2C
The charge Q remains constant, but it will now distribute between the two capacitors.
Step 3: Calculate the new voltage across the combined capacitors.
The voltage across the combined system can be found using the formula for charge:
Q=Ctotal⋅Vnew
Substituting the total capacitance:
Q=2C⋅Vnew
Since Q=CV, we can equate:
CV=2C⋅Vnew
Solving for Vnew:
Vnew=V2
Step 4: Calculate the energy stored in the combined system.
Now, we can calculate the energy stored in the new system:
U2=Q22Ctotal=Q22(2C)=Q24C
Substituting Q=CV:
U2=(CV)24C=CV24
Step 5: Find the ratio of the energies.
Now we can find the ratio of the energy stored in the combined system U2 to the energy stored initially in the single capacitor U1:
Ratio=U2U1=CV24CV22=1/41/2=12
Conclusion:
Thus, the ratio of the energy stored in the combined system to that stored initially in the single capacitor is:
Ratio=1:2
The energy stored in a capacitor is given by the formula:
U1=Q22C
where Q is the charge on the capacitor and C is the capacitance.
Q=CV
Substituting this into the energy formula, we get:
U1=(CV)22C=CV22
When the charged capacitor is connected to an uncharged capacitor of the same capacitance C, the total capacitance of the system becomes:
Ctotal=C+C=2C
The charge Q remains constant, but it will now distribute between the two capacitors.
The voltage across the combined system can be found using the formula for charge:
Q=Ctotal⋅Vnew
Substituting the total capacitance:
Q=2C⋅Vnew
Since Q=CV, we can equate:
CV=2C⋅Vnew
Solving for Vnew:
Vnew=V2
Now, we can calculate the energy stored in the new system:
U2=Q22Ctotal=Q22(2C)=Q24C
Substituting Q=CV:
U2=(CV)24C=CV24
Now we can find the ratio of the energy stored in the combined system U2 to the energy stored initially in the single capacitor U1:
Ratio=U2U1=CV24CV22=1/41/2=12
Thus, the ratio of the energy stored in the combined system to that stored initially in the single capacitor is:
Ratio=1:2
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set- II]
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set-III]
3 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD
4 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
A capacitor of capacitance C0 is charged to potential V0. Now it is connected to another uncharged capacitor of capacitance C02. Calculate the heat loss in this process.
View SolutionAnswer the following:
(a) Describe briefly the process of transferring charge between the two plates of a parallel plate capacitor when connected to a battery. Derive an expression for the energy stored in a capacitor.
(b) A parallel plate capacitor is connected to a battery of potential difference V. It is disconnected from battery and then connected to another uncharged capacitor of the same capacitance. Calculate the ratio of the energy stored in the combination to the initial energy on the single capacitor.
View Solution
Knowledge Check
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
A capacitor of capacitance 2.0μF is charged to a potential difference of 12 V. It is then connected to an uncharged capacitor of capacitance 4.0μF. Find (a) the charge flow through connecting wire upto study strate on each of the two capacitors after the connection in μC (b) The total electrostatic energy stored in both capacitors in μJ (c) the heat produced during the charge transfer from one capacitor to the other in μJ.
View SolutionA parallel plate capacitor of capacity C0 is charged to a potential V0,E1 is the energy stored in the capacitor when the battery is disconnected and the plate separation is doubled, and E2 is the energy stored in the capacitor when the charging battery is kept connected and the separation between the capacitor plates is dounled. find the ratio E1/E2.
View SolutionThe energy stored in a capacitor of capacity C and potential V is given by
View SolutionFind the charged stored in all the capacitors
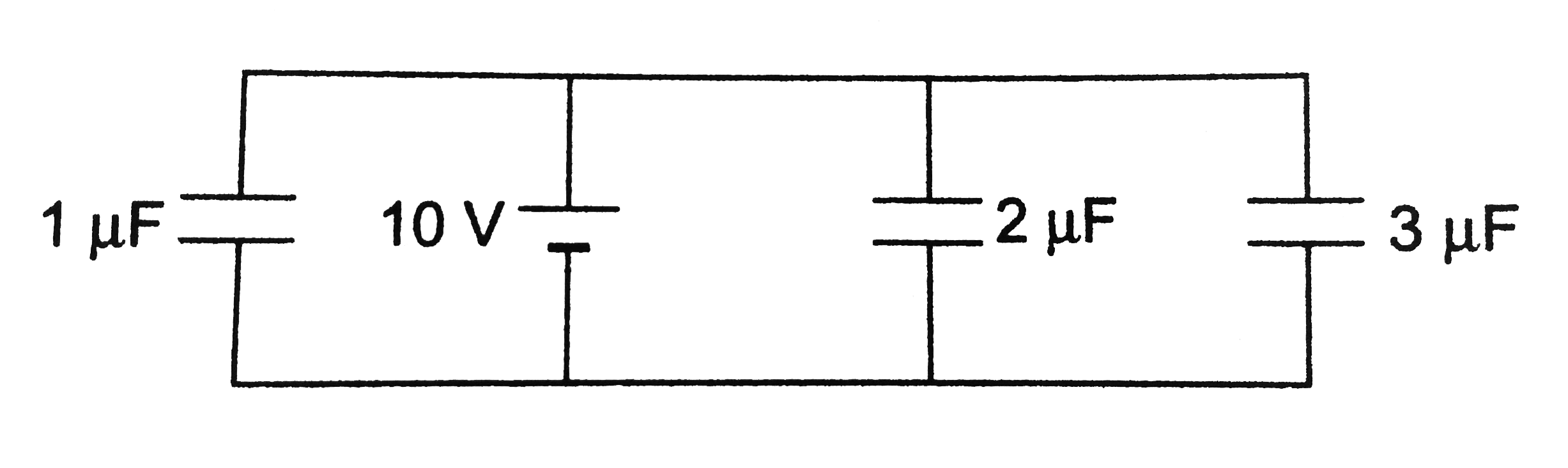
View SolutionA capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
View SolutionA capacitor of capacitor of capacitance 2.0μF is charge to a potential diffrence of 12V It is then connected of uncharged capacitor of capacitance 4.0μF as shown in figure . Find (a ) the charge on each of the two capacitors after the connection, (b ) the electrostatic energy stored in each of the two capacitors.

View SolutionA capacitor of capacitance C is initially charged to a potential difference of V volt. Now it is connected to a battery of 2V with oppoiste polarity. The ratio of heat generated to the final enegry stored in the capacitor will be
View Solution
