An alternating voltage given by V=70sin100πt is connected across a pure resistor of 25Ω. Find
(i) the frequency of the source.
(ii) the rms current through the resistor.
To solve the problem step by step, we will break it down into two parts as required: finding the frequency of the source and calculating the RMS current through the resistor.
Step 1: Find the frequency of the source
1. The given voltage equation is:
V=70sin(100πt)
This can be compared to the general form of an alternating voltage:
V=V0sin(ωt)
where V0 is the peak voltage and ω is the angular frequency.
2. From the given equation, we can identify:
V0=70andω=100π
3. The relationship between angular frequency ω and frequency f is given by:
ω=2πf
4. Substituting the value of ω:
100π=2πf
5. Dividing both sides by 2π:
f=100π2π=50Hz
Step 2: Calculate the RMS current through the resistor
1. The RMS voltage Vrms can be calculated from the peak voltage V0 using the formula:
Vrms=V0√2
2. Substituting the value of V0:
Vrms=70√2=701.414≈49.497V
3. The RMS current Irms through the resistor can be calculated using Ohm's law:
Irms=VrmsR
where R=25Ω.
4. Substituting the values:
Irms=49.49725≈1.97988A≈1.98A
Final Answers:
(i) The frequency of the source is 50Hz.
(ii) The RMS current through the resistor is approximately 1.98A.
---
V=70sin(100πt)
This can be compared to the general form of an alternating voltage:
V=V0sin(ωt)
where V0 is the peak voltage and ω is the angular frequency.
V0=70andω=100π
ω=2πf
100π=2πf
f=100π2π=50Hz
Vrms=V0√2
Vrms=70√2=701.414≈49.497V
Irms=VrmsR
where R=25Ω.
Irms=49.49725≈1.97988A≈1.98A
(i) The frequency of the source is 50Hz.
(ii) The RMS current through the resistor is approximately 1.98A.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET - I
26 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET - II (Delhi Board)
7 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) [SET - II]
6 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
An alternating voltage given by V=140sin314t is connected across a pure resistor of 50 ohm. Find (i) the frequency of the source. (ii) the rms current thought the resistor.
View SolutionAn alternating voltage given by
E=280sin50πt is connected across a pure resistor of 40 ohm. Find frequency of source and rms current through the bulb.
View Solution
Knowledge Check
A alternating voltage given by V=140sin314t is connected across a pure resistor of 50 ohm. Find the rms current through the resistor.
A1.98AB5.63AC3.536AD49.39A
A 120 volt AC source is connected across a pure inductor of inductance 0.70 henry. If the frequency of the source is 60Hz, the current passing through the inductor is
View SolutionWhen a 12V battery is connected across an unknown resistor, there is a current of 2.5mA in the circuit. Find the value of the resistance of the resistor.
View SolutionThe value of escape speed from the surface of earth is
View SolutionIn the circuit shown in fig the voltage across the 6Ω resistor is 12V. What is the emf of the battery and the current thorugh the 6Oemga resistor?
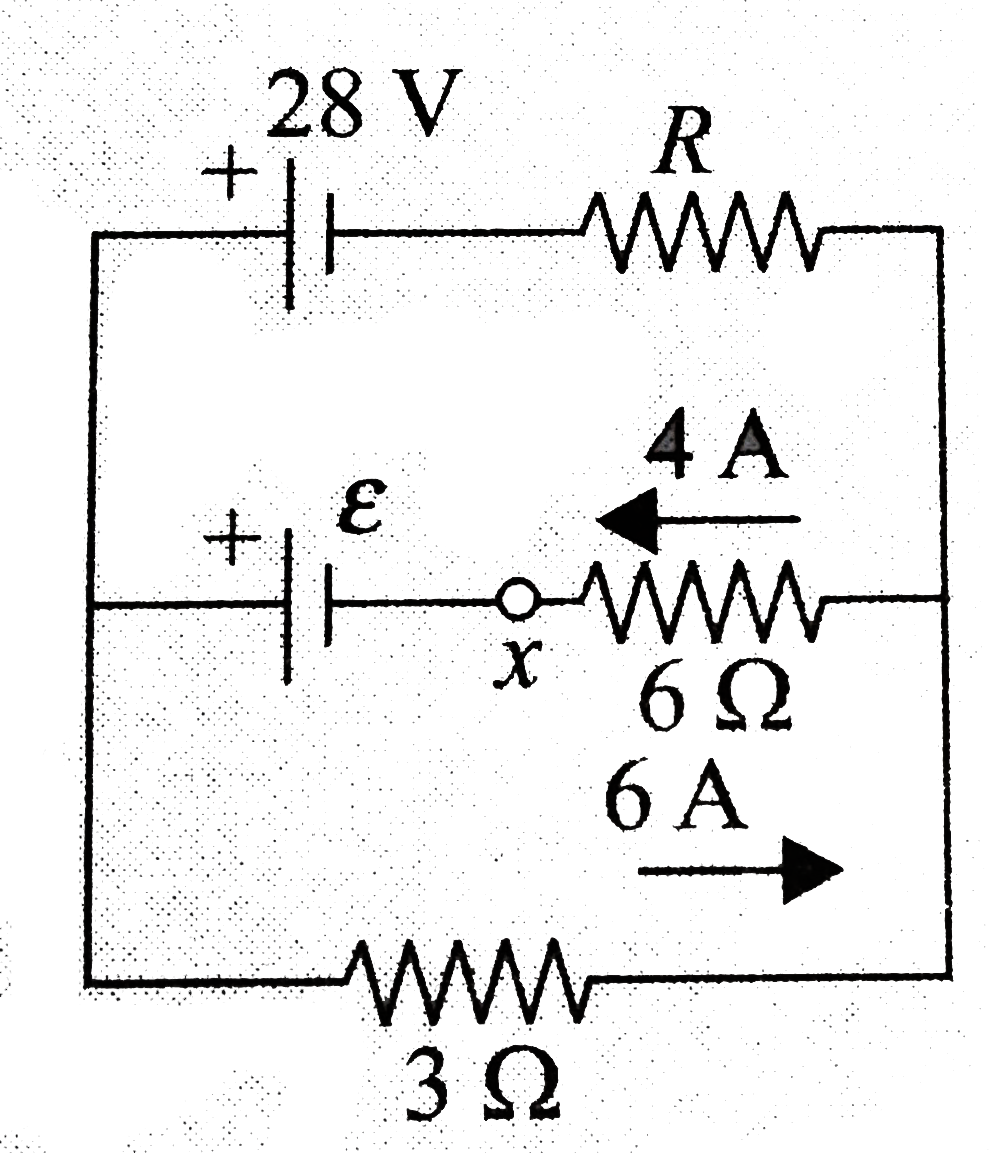
View SolutionAn alternating emf given by equation
e=300sin(100π)tV
is applied to a resistance 100Ω. The rms current through the circuit is (in amperes).
View SolutionA 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
What is the current flowing through the circuit?
View SolutionAn alternating current in a circuit is given by l = 20 sin ( 100πt + 0.05π) A. The rms value and the frequency of current respectively are
View Solution