In a single slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band ?
To analyze how doubling the width of the slit in a single slit diffraction experiment affects the size and intensity of the central diffraction band, we can follow these steps:
Step 1: Understand the formula for the width of the central maximum
The width of the central maximum in a single slit diffraction pattern is given by the formula:
V0=2Dλd
where:
- V0 is the width of the central maximum,
- D is the distance from the slit to the screen,
- λ is the wavelength of the light used,
- d is the width of the slit.
Step 2: Determine the new width of the slit
If the width of the slit is doubled, we can express the new width as:
d′=2d
Step 3: Calculate the new width of the central maximum
Substituting d′ into the formula for the width of the central maximum, we get:
V′0=2Dλd′=2Dλ2d=Dλd
Thus, we can see that:
V′0=V02
This means that the new width of the central maximum is half of the original width.
Step 4: Analyze the intensity of the central maximum
The intensity of the central maximum in a single slit diffraction pattern is given by the formula:
I∝1d2
However, it is important to note that the intensity of the central maximum is independent of the slit width d. Therefore, even when the slit width is doubled, the intensity remains unchanged.
Summary of Results
- The size of the central maximum is halved when the width of the slit is doubled.
- The intensity of the central maximum remains unchanged.
The width of the central maximum in a single slit diffraction pattern is given by the formula:
V0=2Dλd
where:
- V0 is the width of the central maximum,
- D is the distance from the slit to the screen,
- λ is the wavelength of the light used,
- d is the width of the slit.
If the width of the slit is doubled, we can express the new width as:
d′=2d
Substituting d′ into the formula for the width of the central maximum, we get:
V′0=2Dλd′=2Dλ2d=Dλd
Thus, we can see that:
V′0=V02
This means that the new width of the central maximum is half of the original width.
The intensity of the central maximum in a single slit diffraction pattern is given by the formula:
I∝1d2
However, it is important to note that the intensity of the central maximum is independent of the slit width d. Therefore, even when the slit width is doubled, the intensity remains unchanged.
- The size of the central maximum is halved when the width of the slit is doubled.
- The intensity of the central maximum remains unchanged.
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:PHYSICS (Theory) [SET - III]
Explore 9 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SET - I
Explore 26 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:PHYSICS (Theory) [SET - I]
Explore 26 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
(a) Define a wavefront. Using Huygen's principle, verify the laws of reflection at a plane surface .
(b) In a single slit diffraction experiment the wildth of the slit is made double the orignal width.
How does this affect the size and intensity of the central diffraction band ? Explain.
(c) When a tiny circular obstacle in placed in the path of light from a distance source, a bright spot is seen at the centre of the obstacle . Explain why.
View SolutionIn a single-slit diffraction experiment, the width of the slit is made half of the original width:
View Solution
Knowledge Check
In a single slit diffraction experiment, the width of the slit is made double its original width. Then the central maximum of the diffraction pattern will become
Anarrower and fainterBnarrower and brighterCbroader and fainterDbroader and brighter
In a single slit diffraction pattern
View SolutionUse Huygens's principle to explain the formation of diffraction pattern due to a single slit illuminated by a monochromatic source of light.
When the width of the slit is made double the original width, how would this affect the size and intensity of the central diffraction band ?
View SolutionIn single sit diffraction experiment, the width of the central maximum inversely proportional to
View SolutionWhen a plane wave front of light, of wavelength λ, is incident on a narrow slit, an intensity distribution pattern, of the form shown is observed on a screen, suitably kept behind the slit. Name the phenomenon observed.
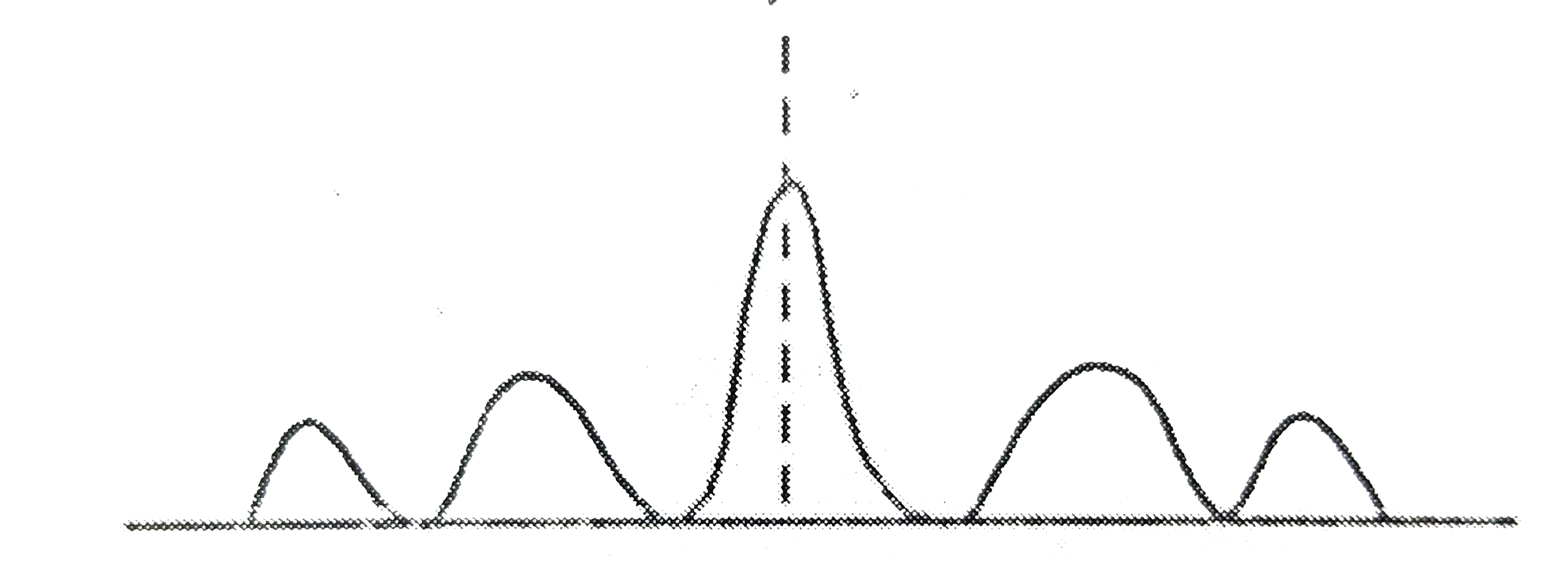
(a) Obtain the conditions for the formation of central maximum and secondary maxima and the minima.
(b) Why is there significant fall in intensity of the secondary maxima compared to the central maximum, whereas in double slit experiment all the bright fringes are of the same intensity ?
(c) When the width of the slit is made double the original width, how is the size of the central band affected ?
View SolutionIn Young's double slit experiment the type of diffractive is
View SolutionIn Young'double-slit interference experiment, if the slit separation is made threefold, the fringe width becomes
View SolutionIn Fraunhofer.s single slit diffraction experiment, how does semi-angular width e of the central bright fringe depend on slit width .a.?
View Solution