Use Huygens's principle to explain the formation of diffraction pattern due to a single slit illuminated by a monochromatic source of light.
When the width of the slit is made double the original width, how would this affect the size and intensity of the central diffraction band ?
Step-by-Step Solution:
1. Understanding Huygens's Principle:
Huygens's principle states that every point on a wavefront can be considered as a source of secondary wavelets that spread out in all directions. The new wavefront is formed by the envelope of these secondary wavelets.
Hint: Recall that Huygens's principle is fundamental in wave theory and helps in understanding wave propagation.
2. Setup of the Experiment:
Consider a single slit of width 'a' illuminated by a monochromatic source of light. When light passes through the slit, it diffracts, and the resulting pattern is observed on a screen placed at a distance 'D' from the slit.
Hint: Visualize the setup with a slit and a screen to understand the diffraction pattern formation.
3. Formation of the Diffraction Pattern:
When light passes through the slit, it can be treated as a collection of wavelets emanating from different points across the width of the slit. The interference of these wavelets leads to the formation of a diffraction pattern characterized by a central maximum and several minima and maxima on either side.
Hint: Think about how wavelets from different parts of the slit interfere constructively and destructively.
4. Condition for Minima:
The condition for minima in the diffraction pattern occurs when the path difference between wavelets from the edges of the slit equals an odd multiple of half wavelengths. Mathematically, this is given by:
asinθ=nλ(n=1,2,3,…)
where θ is the angle of diffraction, a is the slit width, and λ is the wavelength of the light.
Hint: Remember that the path difference is crucial for determining where minima occur.
5. Width of the Central Maximum:
The width of the central maximum can be expressed as:
Width=2λDa
where D is the distance from the slit to the screen.
Hint: This formula shows how the width of the central maximum is inversely proportional to the slit width.
6. Effect of Doubling the Slit Width:
If the width of the slit is doubled (i.e., a becomes 2a), the new width of the central maximum becomes:
New Width=2λD2a=λDa
Thus, the width of the central maximum is halved.
Hint: Analyze how changes in the slit width affect the diffraction pattern dimensions.
7. Effect on Intensity:
The intensity of the central maximum is related to the amplitude of the wavelets. When the slit width is doubled, the intensity of the central maximum increases by a factor of four, as intensity is proportional to the square of the amplitude.
Hint: Consider how the amplitude of the wavelets contributes to the overall intensity observed.
Summary:
- The diffraction pattern is formed due to the interference of wavelets from different parts of the slit.
- Doubling the slit width reduces the size of the central maximum to half and increases its intensity by four times.
Huygens's principle states that every point on a wavefront can be considered as a source of secondary wavelets that spread out in all directions. The new wavefront is formed by the envelope of these secondary wavelets.
Consider a single slit of width 'a' illuminated by a monochromatic source of light. When light passes through the slit, it diffracts, and the resulting pattern is observed on a screen placed at a distance 'D' from the slit.
When light passes through the slit, it can be treated as a collection of wavelets emanating from different points across the width of the slit. The interference of these wavelets leads to the formation of a diffraction pattern characterized by a central maximum and several minima and maxima on either side.
The condition for minima in the diffraction pattern occurs when the path difference between wavelets from the edges of the slit equals an odd multiple of half wavelengths. Mathematically, this is given by:
asinθ=nλ(n=1,2,3,…)
where θ is the angle of diffraction, a is the slit width, and λ is the wavelength of the light.
The width of the central maximum can be expressed as:
Width=2λDa
where D is the distance from the slit to the screen.
If the width of the slit is doubled (i.e., a becomes 2a), the new width of the central maximum becomes:
New Width=2λD2a=λDa
Thus, the width of the central maximum is halved.
The intensity of the central maximum is related to the amplitude of the wavelets. When the slit width is doubled, the intensity of the central maximum increases by a factor of four, as intensity is proportional to the square of the amplitude.
- The diffraction pattern is formed due to the interference of wavelets from different parts of the slit.
- Doubling the slit width reduces the size of the central maximum to half and increases its intensity by four times.
Similar Questions
Knowledge Check
In a single slit diffraction experiment, the width of the slit is made double its original width. Then the central maximum of the diffraction pattern will become
Anarrower and fainterBnarrower and brighterCbroader and fainterDbroader and brighter
(a) Define a wavefront. Using Huygen's principle, verify the laws of reflection at a plane surface .
(b) In a single slit diffraction experiment the wildth of the slit is made double the orignal width.
How does this affect the size and intensity of the central diffraction band ? Explain.
(c) When a tiny circular obstacle in placed in the path of light from a distance source, a bright spot is seen at the centre of the obstacle . Explain why.
View SolutionIn a single-slit diffraction experiment, the width of the slit is made half of the original width:
View SolutionThe first diffraction minima due to a single slit diffraction is at θ=30∘ for a light of wavelength 5000Å The width of the slit is
View SolutionWhen a plane wave front of light, of wavelength λ, is incident on a narrow slit, an intensity distribution pattern, of the form shown is observed on a screen, suitably kept behind the slit. Name the phenomenon observed.
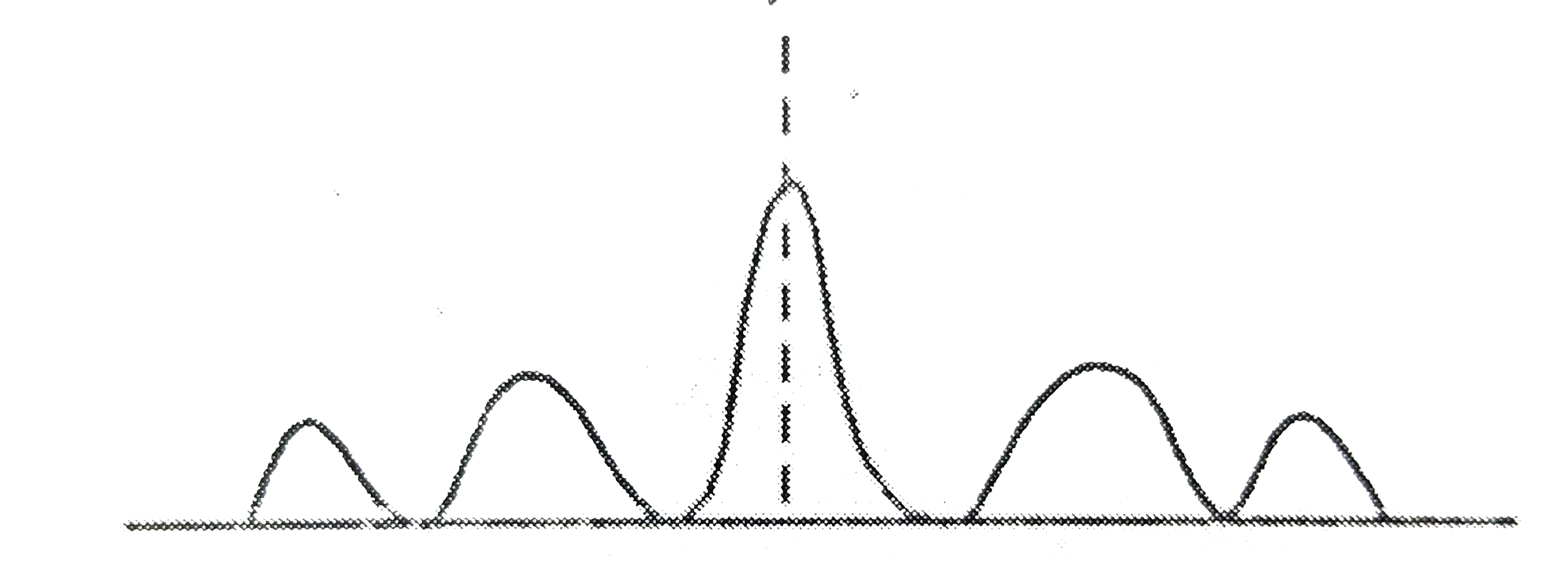
(a) Obtain the conditions for the formation of central maximum and secondary maxima and the minima.
(b) Why is there significant fall in intensity of the secondary maxima compared to the central maximum, whereas in double slit experiment all the bright fringes are of the same intensity ?
(c) When the width of the slit is made double the original width, how is the size of the central band affected ?
View SolutionThe first diffraction minimum due to single slit diffraction is θ for a light of wavelength 5000A if the width of the slit is 1×1021cm then the value of θ is
View SolutionAngular width (β) of central maximum of a diffraction pattern on a single slit does not depend upon
View SolutionDescribe Young's double slit experiment to produce interference pattern due to a monochromatic source of light. Deduce the expression for the fringe width.
View Solution
