A capacitor of capacitance 'C' is being charged by connecting it across a dc source along with an ammeter. Will the ammeter show a momentary deflection during the process of charging? If so, how would you explain this momentary deflection and the resulting continuity of current in the circuit? Write the expression for the current inside the capacitor.
To solve the question step by step, we will analyze the charging process of a capacitor connected to a DC source and the behavior of the ammeter in the circuit.
Step 1: Understanding the Charging Process
When a capacitor of capacitance 'C' is connected to a DC voltage source, it starts to charge. The voltage across the capacitor increases as it accumulates charge.
Hint: Recall that a capacitor stores energy in the form of an electric field when it is charged.
Step 2: Current Flow During Charging
During the initial moment of charging, there is a flow of current in the circuit. This current is due to the movement of charge carriers (electrons) from one plate of the capacitor to the other, creating a potential difference across the capacitor.
Hint: Consider how current is defined and what happens when a potential difference is applied across a circuit.
Step 3: Ammeter Deflection
The ammeter, which measures the current in the circuit, will show a momentary deflection when the capacitor is charging. This deflection occurs because there is a current flowing in the circuit as the capacitor charges.
Hint: Think about what the ammeter measures and how current behaves in a circuit with a changing voltage.
Step 4: Explanation of Momentary Deflection
The momentary deflection of the ammeter can be explained by the concept of displacement current. As the capacitor charges, the electric field between the plates of the capacitor changes, which produces a displacement current. This displacement current is responsible for the continuity of current in the circuit.
Hint: Review the concept of displacement current and how it relates to changing electric fields.
Step 5: Expression for Current in the Capacitor
The current I flowing through the capacitor can be expressed using the relationship between charge Q and capacitance C:
I=dQdt
Since the charge Q on a capacitor is related to the voltage V across it by the equation Q=CV, we can express the current as:
I=CdVdt
This equation shows that the current is proportional to the rate of change of voltage across the capacitor.
Hint: Remember the relationship between charge, voltage, and capacitance when deriving the expression for current.
Summary
1. The ammeter shows a momentary deflection during the charging of the capacitor due to the flow of current.
2. This momentary deflection is explained by the displacement current created by the changing electric field between the capacitor plates.
3. The expression for the current in the capacitor is given by I=CdVdt, indicating that the current depends on the rate of change of voltage across the capacitor.
When a capacitor of capacitance 'C' is connected to a DC voltage source, it starts to charge. The voltage across the capacitor increases as it accumulates charge.
During the initial moment of charging, there is a flow of current in the circuit. This current is due to the movement of charge carriers (electrons) from one plate of the capacitor to the other, creating a potential difference across the capacitor.
The ammeter, which measures the current in the circuit, will show a momentary deflection when the capacitor is charging. This deflection occurs because there is a current flowing in the circuit as the capacitor charges.
The momentary deflection of the ammeter can be explained by the concept of displacement current. As the capacitor charges, the electric field between the plates of the capacitor changes, which produces a displacement current. This displacement current is responsible for the continuity of current in the circuit.
The current I flowing through the capacitor can be expressed using the relationship between charge Q and capacitance C:
I=dQdt
Since the charge Q on a capacitor is related to the voltage V across it by the equation Q=CV, we can express the current as:
I=CdVdt
This equation shows that the current is proportional to the rate of change of voltage across the capacitor.
1. The ammeter shows a momentary deflection during the charging of the capacitor due to the flow of current.
2. This momentary deflection is explained by the displacement current created by the changing electric field between the capacitor plates.
3. The expression for the current in the capacitor is given by I=CdVdt, indicating that the current depends on the rate of change of voltage across the capacitor.
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:PHYSICS (Theory) [SET - II]
Explore 6 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:PHYSICS (Theory) [SET - III]
Explore 9 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:[Set-III]
Explore 3 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
A capacitor of capacitance C, which is initially uncharged , is connected with a battery of emf ε. Find the heat dissipated in the circuit during the process of charging .
View SolutionAn an ideal parallel LC circuit, the capacitor is charged by connecting it to a DC source which is then disconnected. The current in the circuit
View SolutionA parallel capacitor is being charged by an external source. Show that the sum of conductor current and displacement current has the same value everywhere in the circuit.
View SolutionA capacitor of capacitance 25μF is charged to 300V. It is then connected across a 10mH inductor. The resistance in the circuit is negligible.
a. Find the frequency of oscillation of the circuit.
b. Find the potential difference across capacitor and magnitude of circuit current 1.2ms after the inductor and capacitor are connected.
c. Find the magnetic energy and electric energy at t=0 and t=1.2ms.
View SolutionA capacitor of capacitance C is charged to a potential difference V0 and then connected with a resistance and a battery of EMF 3V0 such that the positively charged plate of the capacitor is connected to the positive terminal of the battery. The total heat generated in the resistance until the current in the circuit becomes zero is n(CV20). the value of n is ________.
View SolutionAnswer the following:
(a) When a parallel plate capacitor is connected across a dc battery, explain briefly how the capacitor gets charged.
(b) A parallel plate capacitor of capacitance 'C' is charged to 'V' volt by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant 1<k<2 is introduced to fill the space between the plates. How will the following be affected ?
(i) The electric field between the plates of the capacitor.
(ii) The energy stored in the capacitor. Justify your answer in each case.
(c) The electric potential as a function of distance 'x' is shown in the figure. Draw a graph of the electric field E as a function of x.
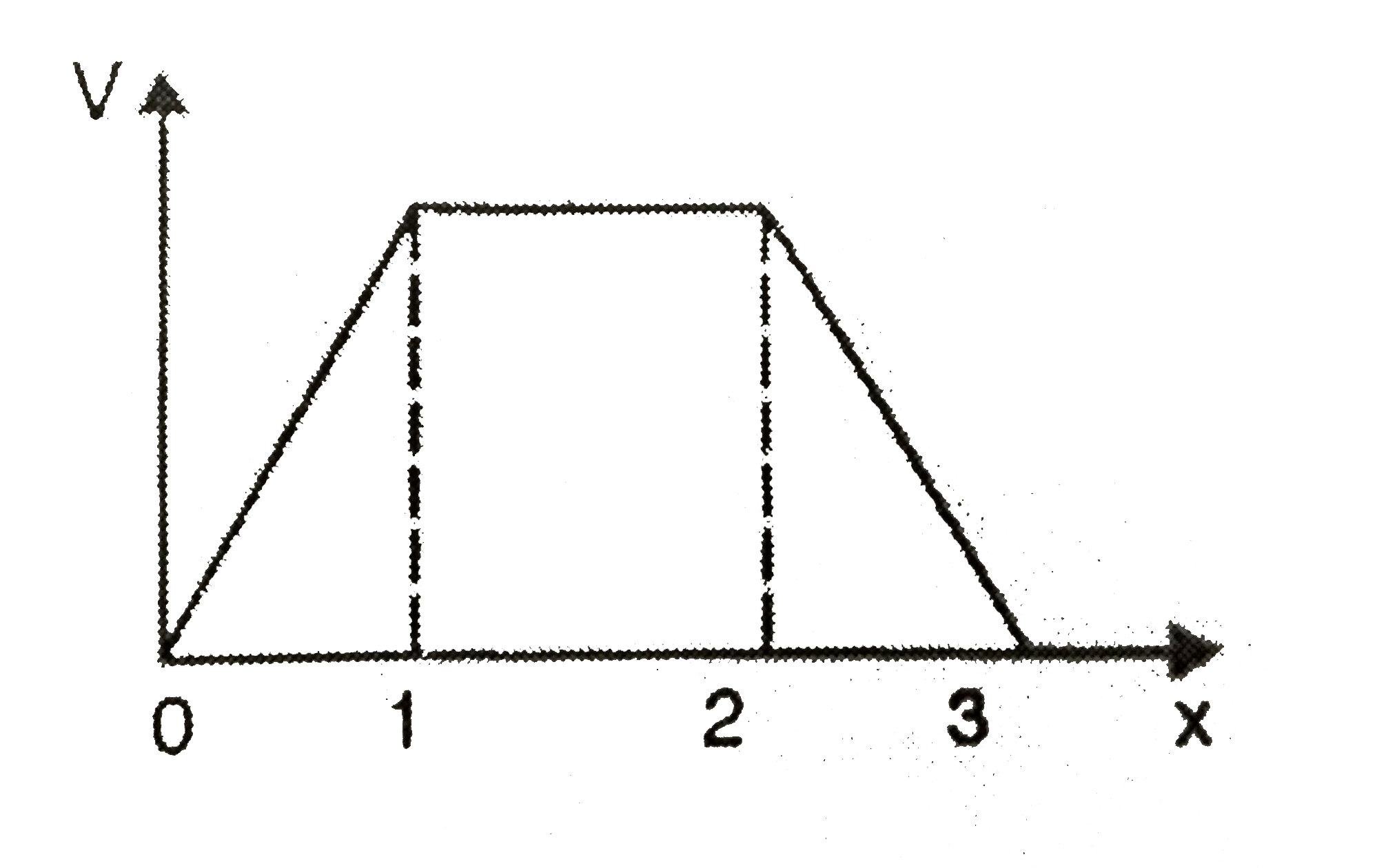
View SolutionA parallel - plate capacitor is being charged.Show that the displacement current across an area in the region between the plates and parallel to it is equal to the conduction current in the connecting wires.
View SolutionA parallel - plate capacitor is being charged.Show that the displacement current across an area in the region between the plates and parallel to it is equal to the conduction current in the connecting wires.
View SolutionTwo capacitor of capacitance 2μFand3μF respectively are charged to potential difference 20 V each. Now the capacitors are connected such that the positively chargd plate of one capacitory is connected to the negatively charged plate of the other. after the current in the circuit has become negligible, the potential difference across the 2μF capacitor is ____V.
View SolutionA capacitor with capacitance 6×10−5F is charged by connecting it to a 12−V battery. The capacitor is disconnected from the battery and connected across an inductor with L=1.50H.
a. What are the angular frequency ω of the electrical oscillations and the period of these oscillations (the time for one oscillation)?
b. What is the intial charge on the capacitor?
c. How much energy is intially stored in the capacitor?
d. What is the charge on the capacitor 0.0230 s after the connecting to the inductor is made? Interpret the sign of the your answer.
e. At the times given in part (d), what is the current in the inductor? Interpret the sign of your answer.
f. At the time given in part (d), how much electrical energy is stored in the capactior and how much is stored in the inductor?
View Solution

