Question

How is a wavefront defined? Using Huygen's construction , draw a figure showing the propagation of a plane wave refracting at a plane surface separating two media. Hence verify Snell's law of refraction.

Explanation

Step-by-Step Solution:

Step 1: Define Wavefront
A wavefront is defined as the locus of all points in a medium that are vibrating in the same phase of a wave. In simpler terms, it is an imaginary surface that connects all the points that are at the same stage of their oscillation.

Step 2: Huygens' Principle
According to Huygens' principle, every point on a wavefront can be considered as a source of secondary wavelets. The new wavefront at a later time can be constructed by drawing a tangent to these wavelets.

Step 3: Draw the Initial Wavefront
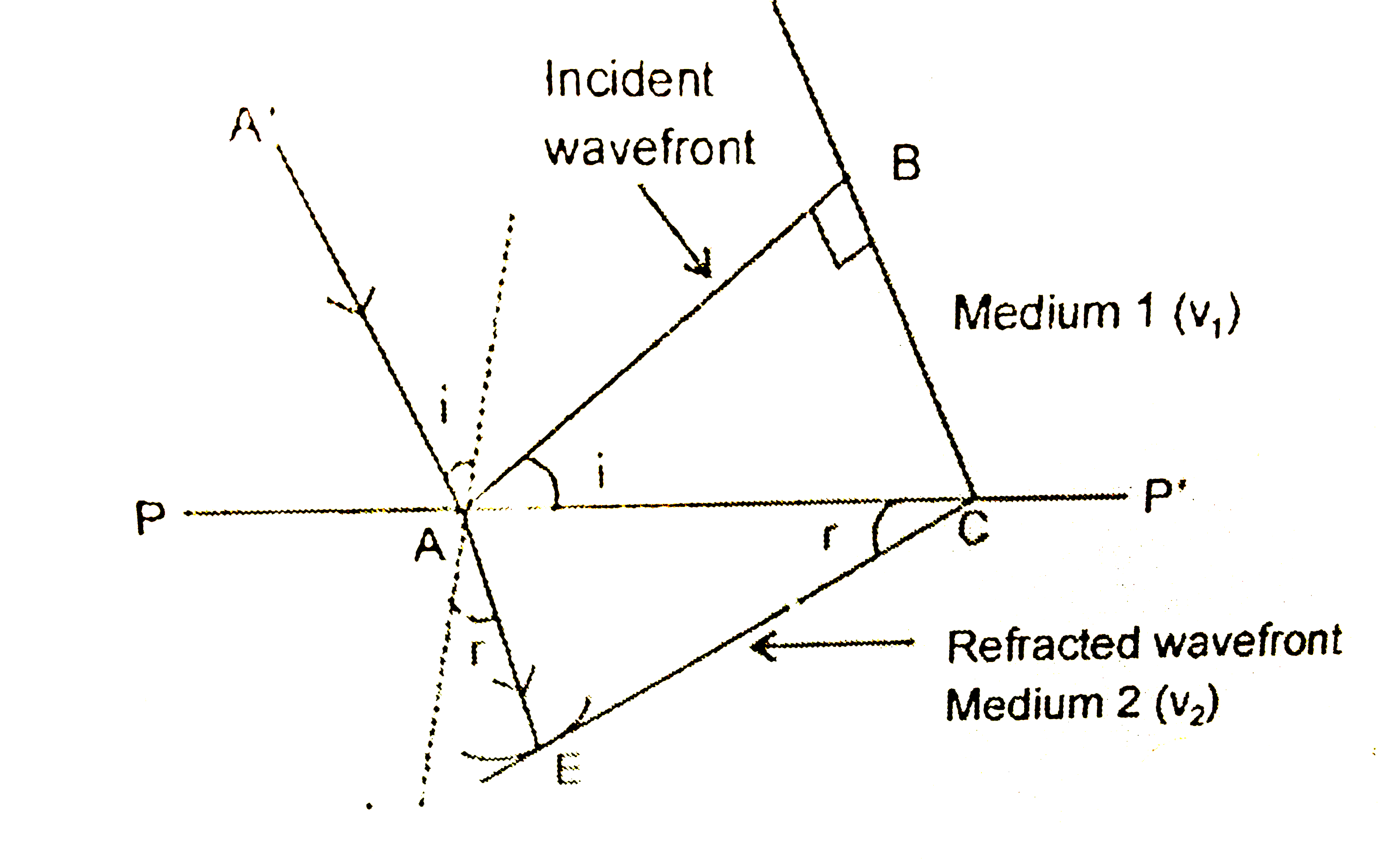
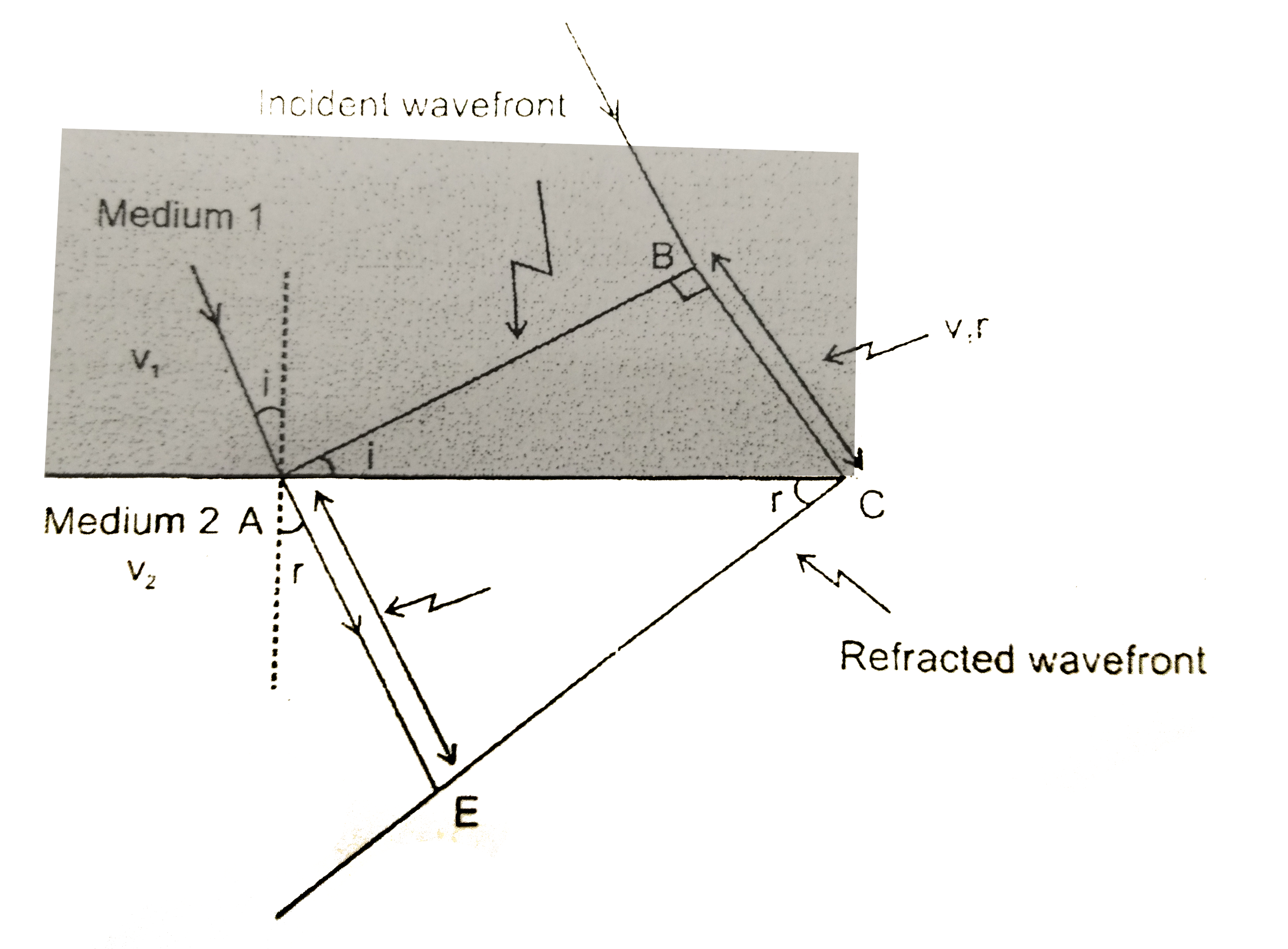
Consider a plane wavefront AB traveling from medium 1 (with speed \( V_1 \)) into medium 2 (with speed \( V_2 \)). At time \( t = 0 \), the wavefront is represented by a straight line AB.

Step 4: Propagation of the Wavefront
After a time \( t \), point A moves to point A' in medium 1 and point B moves to point B' in medium 2. The distances traveled are:
- \( AA' = V_1 t \) in medium 1
- \( BB' = V_2 t \) in medium 2

Step 5: Construct Right Triangles
From the points A, A', B, and B', we can form two right triangles:
1. Triangle ABB' where:
- \( AB' \) is the hypotenuse
- \( \angle I \) is the angle of incidence
2. Triangle AA'B where:
- \( AA' \) is the opposite side
- \( \angle R \) is the angle of refraction

Step 6: Apply Trigonometric Ratios
Using the definitions of sine in the right triangles:
- For triangle ABB':
\( \sin I = \frac{BB'}{AB'} \)
where \( BB' = V_1 t \).

- For triangle AA'B:
\( \sin R = \frac{AA'}{AB'} \)
where \( AA' = V_2 t \).

Step 7: Relate the Two Equations
From the two equations, we can express:
\( \frac{\sin I}{\sin R} = \frac{BB'}{AA'} = \frac{V_1 t}{V_2 t} \)
The \( t \) cancels out, leading to:
\( \frac{\sin I}{\sin R} = \frac{V_1}{V_2} \)

Step 8: Conclusion
This relationship is known as Snell's Law of Refraction, which states:
\( \sin I / \sin R = V_1 / V_2 \)
Thus, we have verified Snell's law using Huygens' construction.

---