The electrostatic potential on the surface of a charged concducting sphere is 100V. Two statements are made in this regard
S1: at any inside the sphere, electric intensity is zero.
S2: at any point inside the sphere, the electrostatic potential is 100V.
S1 is true but S2 is false.
Both S1 and S2 are false.
S1 is true,S2 is also true and S1 is the cause of S2.
S1 is true, S2 is also true but the statements are independent.
The correct Answer is:C
To solve the question, we need to analyze the two statements regarding the electrostatic potential and electric field inside a charged conducting sphere.
1. Understanding the Conducting Sphere:
- A conducting sphere with a charge will have its charge distributed uniformly on its surface. The electric field inside a conductor in electrostatic equilibrium is zero.
2. Analyzing Statement S1:
- Statement S1: "At any point inside the sphere, electric intensity is zero."
- According to Gauss's law, the electric field inside a charged conducting sphere is zero because there is no charge enclosed within a Gaussian surface drawn inside the sphere. Therefore, S1 is true.
3. Analyzing Statement S2:
- Statement S2: "At any point inside the sphere, the electrostatic potential is 100 V."
- The potential inside a conductor is constant and equal to the potential on its surface. Since the potential on the surface of the sphere is given as 100 V, the potential at any point inside the sphere must also be 100 V. Therefore, S2 is also true.
4. Conclusion:
- Both statements S1 and S2 are correct. S1 is true because the electric field inside the sphere is zero, and S2 is true because the potential remains constant throughout the conducting sphere and is equal to the surface potential.
Final Answer:
Both statements S1 and S2 are true.
- A conducting sphere with a charge will have its charge distributed uniformly on its surface. The electric field inside a conductor in electrostatic equilibrium is zero.
- Statement S1: "At any point inside the sphere, electric intensity is zero."
- According to Gauss's law, the electric field inside a charged conducting sphere is zero because there is no charge enclosed within a Gaussian surface drawn inside the sphere. Therefore, S1 is true.
- Statement S2: "At any point inside the sphere, the electrostatic potential is 100 V."
- The potential inside a conductor is constant and equal to the potential on its surface. Since the potential on the surface of the sphere is given as 100 V, the potential at any point inside the sphere must also be 100 V. Therefore, S2 is also true.
- Both statements S1 and S2 are correct. S1 is true because the electric field inside the sphere is zero, and S2 is true because the potential remains constant throughout the conducting sphere and is equal to the surface potential.
Both statements S1 and S2 are true.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - MCQ s (More than one Options)
7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Very short type question
5 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - LONG ANSWER
5 Videos
- MAGNETISM AND MATTER BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - All Questions
24 Videos
Similar Questions
The electric potential on the surface of a sphere of radius R and charge 3×10−6 C is 500 V The intensity of electric field on the surface of the sphere ( inNC−1) is
View SolutionThe electrostatic potential V at any point (x, y, z) in space is given by V=4x2
View SolutionPotential at a point x-distance from the centre inside the conducting sphere of radius R and charged with charge Q is
View SolutionA point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad R(<r). The potential at any point on the sphere is
View SolutionAn insulating solid sphere of radius R has a uniformly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: When a charge 'q' is taken from the centre to the surface of the sphere, its potential energy changes by qρ3∈0
Statement-2 : The electric field at a distance r(r<R) from the centre of the the sphere is ρr3∈0
View SolutionThree plates A, B and C are placed close to each other with +Q charge given to the middle plate. The inner surfaces to A and C can be connected to earth through plate D and keys K1 and K2 . The plates D is a dielectric slab with dielectric constant K1 then the charge that will flow through plate D and keys K1 and K2 . The plate D is a dielectric slab with dielectric constant K, then the charge that will flow though plate D when K2 is closed and K2 is open is
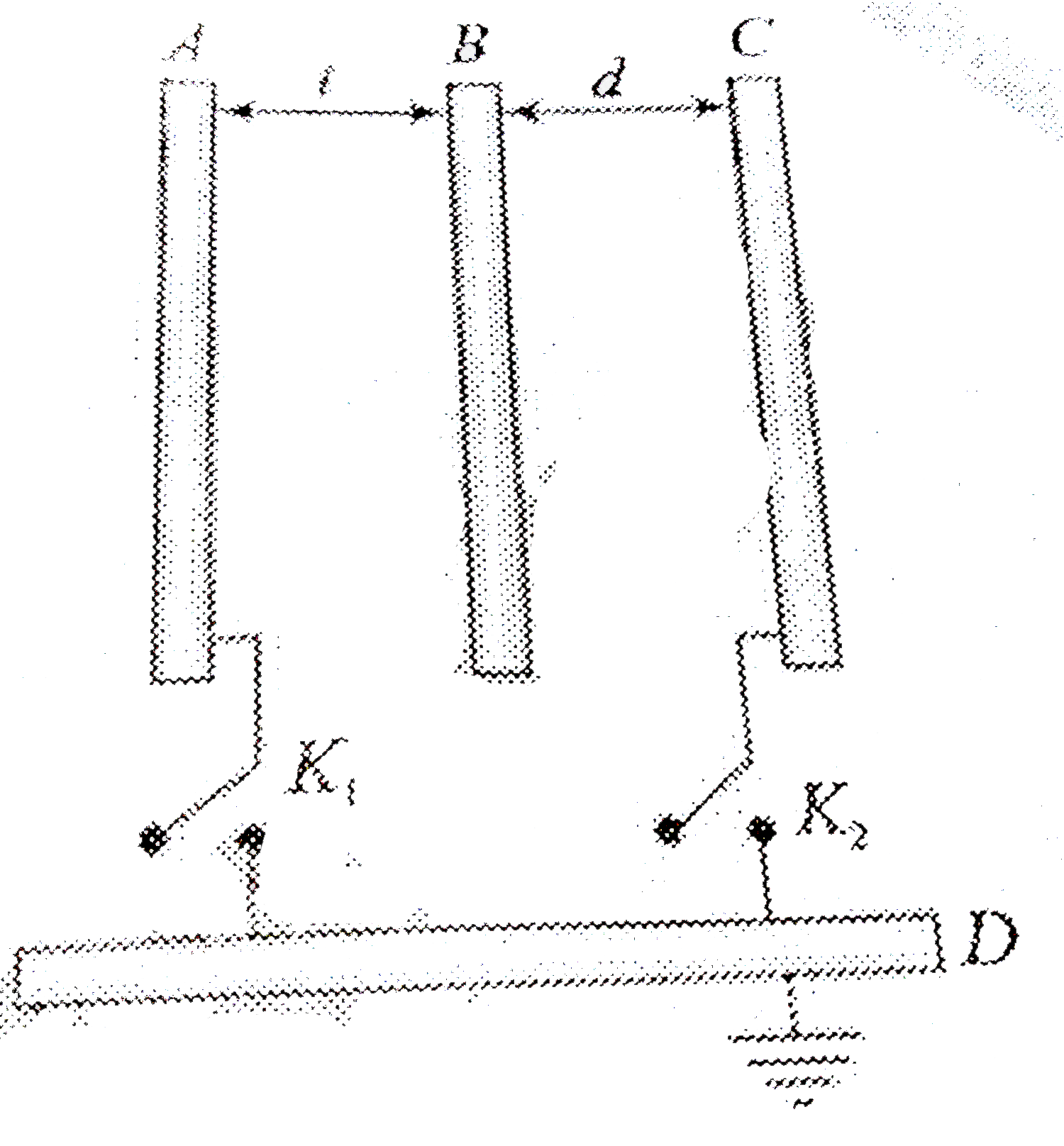
View SolutionA solid insulating sphere of radius R is given a charge Q. If at a point inside the sphere the potential is 1.5 times the potential at the surface, this point will be
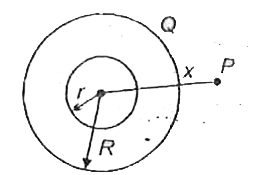
View SolutionTwo concentric hollow conducting spheres of radius r and R are shown. The charge on outer shell is Q. what charge should be given to inner sphere so that the potential at any point P outside the outer sphere is zero ?
View SolutionIf the potential at the centre of a uniformly charged hollow sphere of radius R is V, then electric field at a distance r from the centre of sphere will be (r>R).

View SolutionA hollow charged metal sphere has radius r. If the potential difference between its surface and a point at a distance 3r from the centre is V, then electric field intensity at a distance 3r is
View Solution
