Question

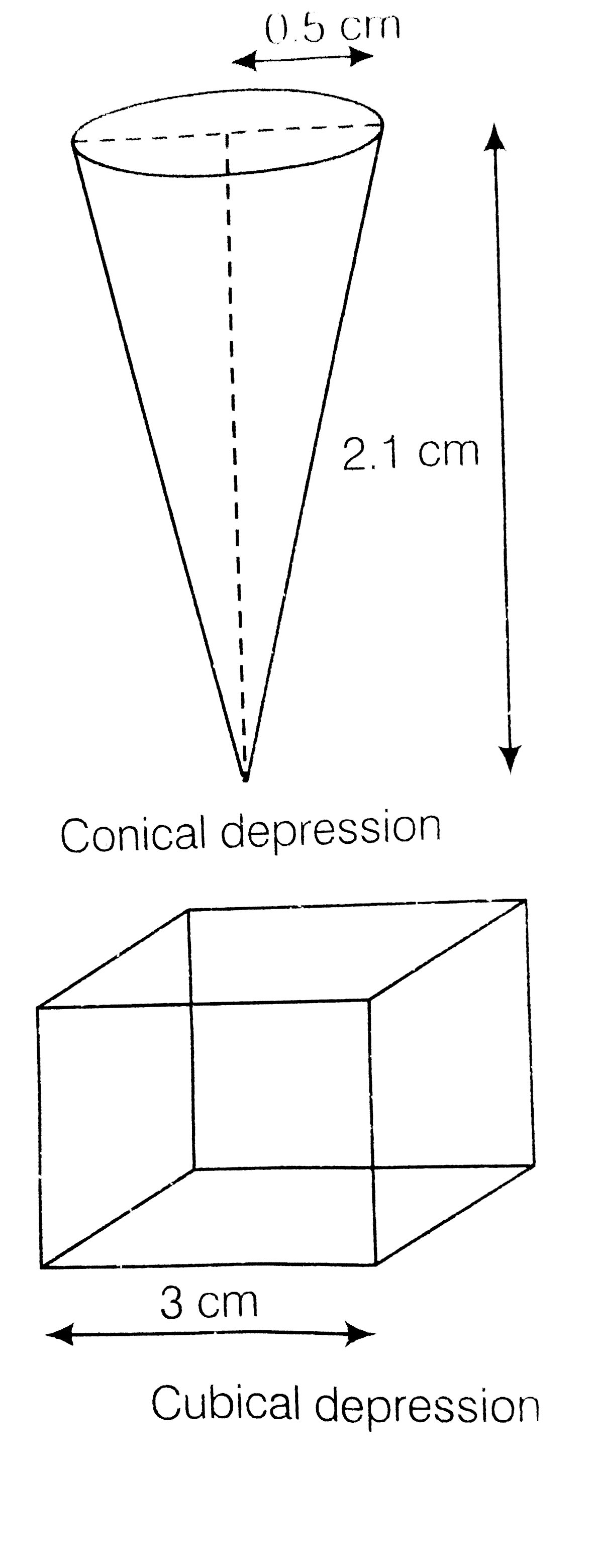
A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimension of the cuboid are 10 cm, 5 cm and 4 cm.The radius of the each of the conical depression is 0.5 cm and depth is 2.1 cm . The edge of the conical depression is 3 cm. Find the volume of the wood in the entire stand.

Explanation

To find the volume of the wood in the pen stand, we will follow these steps:

Step 1: Calculate the volume of the cuboid (pen stand).
The formula for the volume of a cuboid is:
\( \text{Volume of cuboid} = \text{Length} \times \text{Breadth} \times \text{Height} \)
Given dimensions:
- Length (L) = 10 cm
- Breadth (B) = 5 cm
- Height (H) = 4 cm

Substituting the values:
\( \text{Volume of cuboid} = 10 \times 5 \times 4 = 200 \, \text{cm}^3 \)

Step 2: Calculate the volume of one conical depression.
The formula for the volume of a cone is:
\( \text{Volume of cone} = \frac{1}{3} \pi r^2 h \)
Where:
- Radius (r) = 0.5 cm
- Height (h) = 2.1 cm
- Using \(\pi \approx \frac{22}{7}\)

Substituting the values:
\( \text{Volume of one cone} = \frac{1}{3} \times \frac{22}{7} \times (0.5)^2 \times 2.1 \)
Calculating \( (0.5)^2 = 0.25 \):
\( = \frac{1}{3} \times \frac{22}{7} \times 0.25 \times 2.1 \)
Calculating \( 0.25 \times 2.1 = 0.525 \):
\( = \frac{1}{3} \times \frac{22 \times 0.525}{7} \)
Calculating \( 22 \times 0.525 = 11.55 \):
\( = \frac{11.55}{21} \approx 0.55 \, \text{cm}^3 \)

Step 3: Calculate the volume of four conical depressions.
Since there are four conical depressions:
\( \text{Volume of four cones} = 4 \times \text{Volume of one cone} = 4 \times 0.55 = 2.2 \, \text{cm}^3 \)

Step 4: Calculate the volume of the cubical depression.
The formula for the volume of a cube is:
\( \text{Volume of cube} = \text{Edge}^3 \)
Given edge = 3 cm:
\( \text{Volume of cube} = 3^3 = 27 \, \text{cm}^3 \)

Step 5: Calculate the volume of the wood in the pen stand.
Now, we can find the volume of the wood by subtracting the volumes of the conical and cubical depressions from the volume of the cuboid:
\( \text{Volume of wood} = \text{Volume of cuboid} - \text{Volume of four cones} - \text{Volume of cube} \)
Substituting the values:
\( \text{Volume of wood} = 200 - 2.2 - 27 \)
Calculating:
\( = 200 - 29.2 = 170.8 \, \text{cm}^3 \)

Final Answer:
The volume of the wood in the entire pen stand is \( 170.8 \, \text{cm}^3 \).

---