Consider sunlight incident on a pinhole of width 103Å. The image of the pinhole seen on a screen shall be
a sharp white ring
different from a geometrical image
a diffused central spot, white in colour
diffused coloured region around a sharp central white spot
The correct Answer is:B, D
To solve the problem of how the image of a pinhole of width 103Å (angstroms) appears on a screen when sunlight is incident on it, we can follow these steps:
1. Convert the Width of the Pinhole:
The width of the pinhole is given as 103Å.
1Å=10−10m⟹103Å=103×10−10m=10−7m
Hint: Always convert units to standard SI units for calculations.
2. Understand the Wavelength of Sunlight:
The wavelength of sunlight ranges from approximately 400nm to 700nm.
400nm=4×10−7mand700nm=7×10−7m
Hint: Knowing the range of wavelengths helps in understanding diffraction effects.
3. Compare Pinhole Width and Wavelength:
The width of the pinhole 10−7m is comparable to the wavelengths of sunlight, which range from 4×10−7m to 7×10−7m. This indicates that diffraction will occur since the width of the slit is less than or equal to the wavelength of light.
Hint: Diffraction occurs when the size of the aperture is on the order of the wavelength of the light.
4. Describe the Diffraction Pattern:
When light passes through the pinhole, it will diffract. The central spot will appear white due to the combination of all colors of light, while the edges will show a spectrum of colors due to the different wavelengths bending at different angles.
Hint: The central spot is a result of constructive interference, while the colors around it result from the varying degrees of diffraction.
5. Conclusion on the Image:
The image on the screen will consist of a diffuse central white spot surrounded by colored regions. The central spot is white because it is the result of all colors combining, and the surrounding colors are due to the diffraction of different wavelengths.
Hint: Remember that the image formed is not a sharp geometrical image but a result of wave phenomena.
Final Answer:
The image of the pinhole will be a diffuse central white spot with colored regions surrounding it, confirming that the correct options are:
- A diffuse central spot (white in color)
- Diffused colored regions around the sharp central spot.
The width of the pinhole is given as 103Å.
1Å=10−10m⟹103Å=103×10−10m=10−7m
The wavelength of sunlight ranges from approximately 400nm to 700nm.
400nm=4×10−7mand700nm=7×10−7m
The width of the pinhole 10−7m is comparable to the wavelengths of sunlight, which range from 4×10−7m to 7×10−7m. This indicates that diffraction will occur since the width of the slit is less than or equal to the wavelength of light.
When light passes through the pinhole, it will diffract. The central spot will appear white due to the combination of all colors of light, while the edges will show a spectrum of colors due to the different wavelengths bending at different angles.
The image on the screen will consist of a diffuse central white spot surrounded by colored regions. The central spot is white because it is the result of all colors combining, and the surrounding colors are due to the diffraction of different wavelengths.
The image of the pinhole will be a diffuse central white spot with colored regions surrounding it, confirming that the correct options are:
- A diffuse central spot (white in color)
- Diffused colored regions around the sharp central spot.
Topper's Solved these Questions
- WAVE OPTICSBook:NCERT EXEMPLAR ENGLISHChapter:WAVE OPTICSExercise:Very short Answer Type Questions.
Explore 6 Videos
- WAVE OPTICSBook:NCERT EXEMPLAR ENGLISHChapter:WAVE OPTICSExercise:Short answer type Questions
Explore 3 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIAL,DEVICES AND SIMPLE CIRCUITBook:NCERT EXEMPLAR ENGLISHChapter:SEMICONDUCTOR ELECTRONICS: MATERIAL,DEVICES AND SIMPLE CIRCUITExercise:Multiplel choice questions
Explore 26 Videos
Similar Questions
Consider sunlight incident on a slit of width 104Å . The image seen through the slit shall
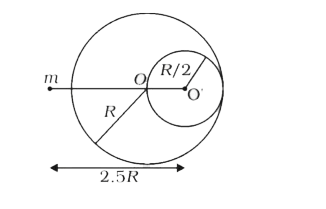
View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?
View Solution
Knowledge Check
Consider sunlight incident on a slit of width 104Å . The image seen through the slit shall
Abe a fine sharp slit white in colour at the centreBa bright slit white at the centre diffusing to zero intensities at the edgesCa bright slit white at the centre diffusing to regions of different coloursDonly be a diffused slit white in colourConsider sunlight incident on a slit of width 104Å . The image seen through the slit shall
Abe a fine sharp slit white in colour at the centreBa bright slit white at the centre diffusing to zero intensities at the edgesCa bright slit white at the centre diffusing to regions of different coloursDonly be a diffused slit white in colour
The image formed by a pinhole camera is
View SolutionConsider the diffraction pattern for a small pinhole. As the size of the hole is increased
View SolutionLight of wavelength 5000 Å is incident on a slit of width 0.1 mm. Find out the width of the central bright line on a screen distance 2m from the slit?
View SolutionLight of wavelength 6328Å is incident normally on a slit of width 0.2 mm. Angular width of the central maximum on the screen will be :
View SolutionLight of wavelength λ is incident on a slit width d. The resulting diffraction pattern is observed on a screen at a distance D. The linear width of the principal maximum is then equal to the width of the slit if D equals
View SolutionA monochromatic light of λ=5000Å is incident on two identical slits separated by a distance of 5×10−4 m. The interference pattern is seen on a screen placed at a distance of 1 m from the plane of slits. A thin glass plate of thickness 1.5×10−6 m and refractive index μ=1.5 is placed between one of the slits and the screen . Find the intensity at the center of the screen.
View Solution

