Do magnetic forces obey Newton's third law. Verify for two current elements d→l1=dlˆi located at the origin and d→l2=dlˆj located at (0, R, 0). Both carry current I.
To verify whether magnetic forces obey Newton's third law for the given current elements, we will follow these steps:
Step 1: Define the Current Elements
We have two current elements:
- d→l1=dl^i located at the origin (0, 0, 0).
- d→l2=dl^j located at (0, R, 0).
Both carry a current I.
Step 2: Calculate the Magnetic Field due to d→l1 at the Location of d→l2
Using the Biot-Savart law, the magnetic field →B1 at the position of d→l2 (0, R, 0) due to the current element d→l1 can be calculated as:
→B1=μ0I4πd→l1×^rr2
Where ^r is the unit vector pointing from d→l1 to d→l2 and r is the distance between them.
The distance r is R, and the unit vector ^r from (0,0,0) to (0,R,0) is ^j. Thus:
→B1=μ0I2πR^k
Step 3: Calculate the Force on d→l2 due to →B1
The force →F2 on the current element d→l2 in the magnetic field →B1 is given by:
→F2=Id→l2×→B1
Substituting d→l2=dl^j and →B1=μ0I2πR^k:
→F2=I(dl^j)×(μ0I2πR^k)
Using the right-hand rule, we find:
→F2=μ0I2dl2πR^i
Step 4: Calculate the Magnetic Field due to d→l2 at the Location of d→l1
Now, we calculate the magnetic field →B2 at the origin (0, 0, 0) due to d→l2:
→B2=μ0I4πd→l2×^rr2
Here, r=R and ^r points from (0,R,0) to (0,0,0), which is −^j. Thus:
→B2=0
since d→l2 is parallel to ^j and ^r is also along −^j.
Step 5: Calculate the Force on d→l1 due to →B2
Since →B2=0:
→F1=Id→l1×→B2=0
Step 6: Conclusion
From the calculations:
- The force →F2 on d→l2 is μ0I2dl2πR^i.
- The force →F1 on d→l1 is 0.
Since →F1 and →F2 are not equal and opposite, we conclude that magnetic forces do not obey Newton's third law.
We have two current elements:
- d→l1=dl^i located at the origin (0, 0, 0).
- d→l2=dl^j located at (0, R, 0).
Using the Biot-Savart law, the magnetic field →B1 at the position of d→l2 (0, R, 0) due to the current element d→l1 can be calculated as:
→B1=μ0I4πd→l1×^rr2
Where ^r is the unit vector pointing from d→l1 to d→l2 and r is the distance between them.
→B1=μ0I2πR^k
The force →F2 on the current element d→l2 in the magnetic field →B1 is given by:
→F2=Id→l2×→B1
Substituting d→l2=dl^j and →B1=μ0I2πR^k:
→F2=I(dl^j)×(μ0I2πR^k)
Using the right-hand rule, we find:
→F2=μ0I2dl2πR^i
Now, we calculate the magnetic field →B2 at the origin (0, 0, 0) due to d→l2:
→B2=μ0I4πd→l2×^rr2
Here, r=R and ^r points from (0,R,0) to (0,0,0), which is −^j. Thus:
→B2=0
since d→l2 is parallel to ^j and ^r is also along −^j.
Since →B2=0:
→F1=Id→l1×→B2=0
From the calculations:
- The force →F2 on d→l2 is μ0I2dl2πR^i.
- The force →F1 on d→l1 is 0.
Topper's Solved these Questions
- MOVING CHARNGES AND MAGNETISMBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Long Answer Type Questions
7 Videos
- MOVING CHARNGES AND MAGNETISMBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Very Short Answer Type Question
5 Videos
- MAGNETISM AND MATTER BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - All Questions
24 Videos
- NUCLEIBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - NUCLEIEXERCISE - Long answer type question
10 Videos
Similar Questions
Two infinitely long straight wires lie in the xy-plane along the lines x=±R. The wire located at x=+R carries a constant current I1 and the wire located at x=−R carries a constant current I2. A circular loop of radius R is suspended with its centre at (0,0,√3R) and in a plane parallel to the xy-plane. This loop carries a constant current ? in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the +ˆJ direction. Which of the following statements regarding the magnetic field →B is (are) true?
View SolutionTwo parallel wires in the plane of the paper are distance X0 apart. A point charge is moving with speed u between the wires in the same plane at a distance X1 from one of the wires. When the wires carry current of magnitude I in the same direction, the radius of curvature of the path of the point charge is R1 In contrast, if the currents I in the two wires have directions opposite to each other, the radius of curvature of the path is R2. If X0X1=3, the value of R1R2 is
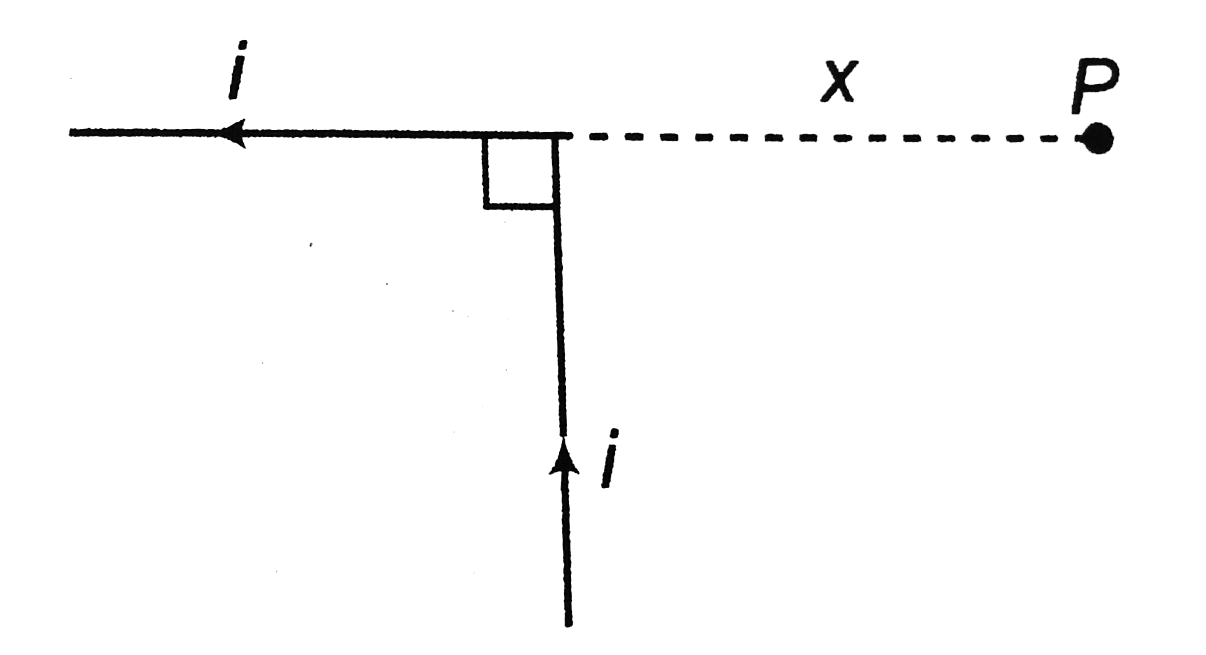
View SolutionDetermine the magnetic field at point P located a distance x from the corner of an infinitely long 2. Wire bent at right angle as shown in figure. The wire carries a steady current i.
View SolutionA rigid wire consists of a semicircular portion of radius R and two straight sections the wire is partially immersed in a perpendicualr magnetic field B as shown in the figure. Find the magnetic force on the wire if it carries a current i.
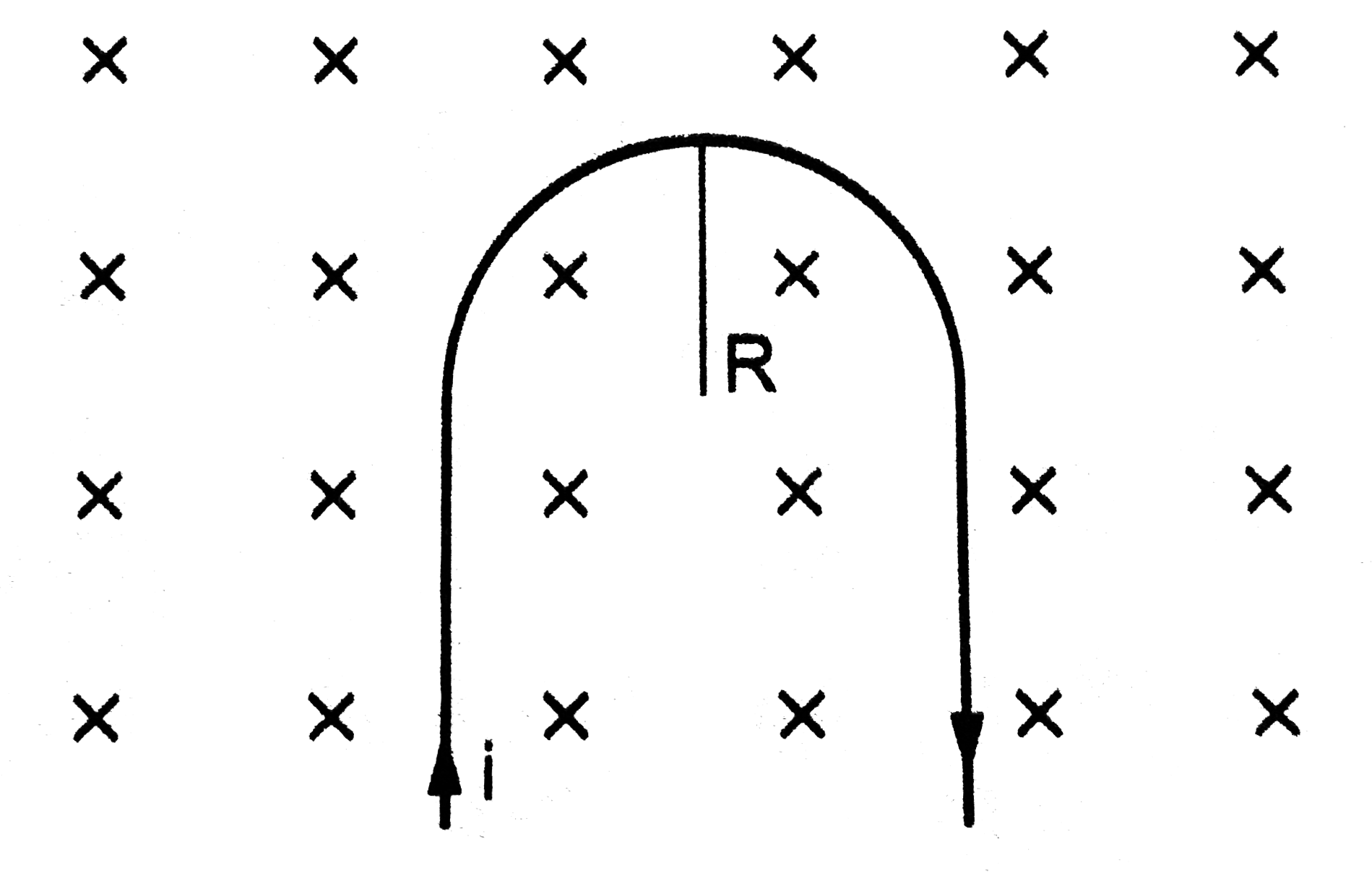
View SolutionThe magnetic field at a distance r from a long wire carryimg current I is 0.4 T. The magnetic field at a distance 2r is
View SolutionFigure. Shows two long wires carrying equal currents I1andI2 flowing in opposite directions. Which of the arrows labeled A to D correctely represents the direction of the magnetic field due to the wires at a point located at an equal distance d from each wire?
View SolutionA: When currents vary with time, Newton's third law is valid only if momentum carried by the electromagnetic field is taken into account.
R: Magnetic field lines always form closed loops.
View SolutionWire 1 in Fig. is oriented along the y-axis and carries a steady current I1. A rectangular loop located to right of the wire and in the x-y plane carries a current I2. Find the magnetic force exerted by wire (1) on the top of wire (2) of length b in the loop, labeled "wire (2)" in the figure.
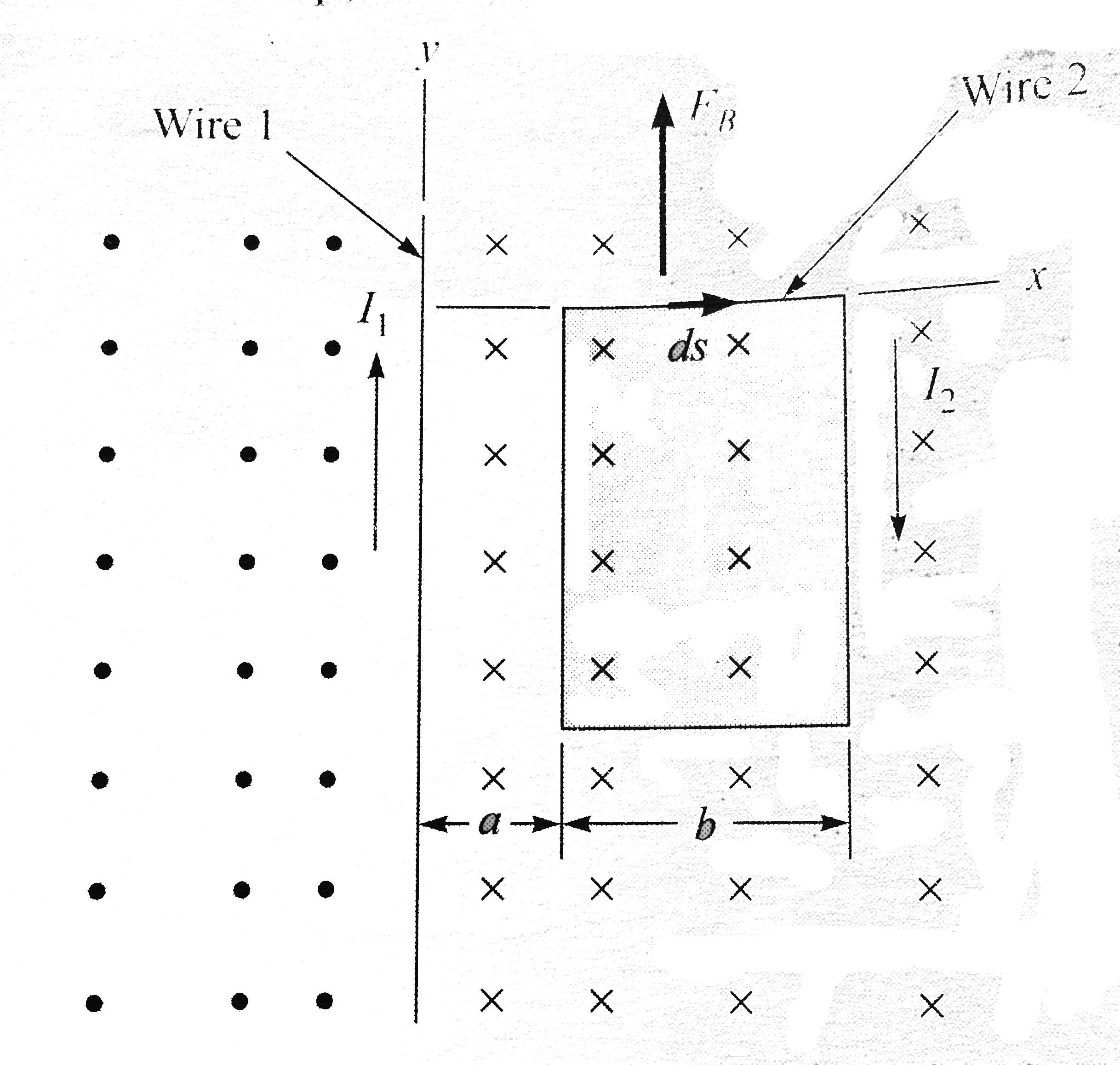
View SolutionFigure shows a long and thin strip of width b which carries a current I. Find magnetic induction due to the current in strip at point P located at a distance r from the strip in the plane of strip as shown in figure-4.35.

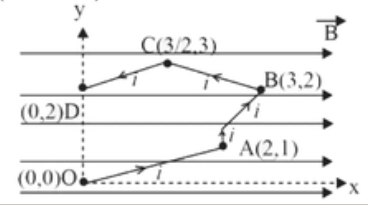
View SolutionA uniform magnetic field →B of magnitude 0.2 T exists in the plane of paper from left to right. A conducting wire, bent in an irregular manner, and carrying a current i , equal to 5A is placed in the plane of paper as shown in figure. Force acting on the wire (in Newton) is
View Solution
