Power is to be delivered to a device via transmission cables having resistance . If is the voltage across and the current through it , find the power wasted and how can it be reduced.
To solve the problem of power wastage in transmission cables, let's break it down step by step.
Step 1: Understanding Power in Transmission Lines
The power wasted in the transmission lines can be expressed using the formula:
Pwasted=I2Rc
where:
- Pwasted is the power wasted in the transmission cables,
- I is the current flowing through the cables,
- Rc is the resistance of the transmission cables.
Step 2: Power Delivered to the Device
The power delivered to the device can be calculated using the formula:
P=V⋅I
where:
- P is the total power delivered to the device,
- V is the voltage across the device,
- I is the current flowing through the device.
Step 3: Analyzing Power Wastage
From the formula for power wasted, we can see that the power wasted is directly proportional to the square of the current (I2). This means that if the current increases, the power wasted in the transmission lines also increases significantly.
Step 4: Reducing Power Wastage
To reduce the power wasted in the transmission lines, we can either:
1. Increase the Voltage: By transmitting power at a higher voltage, we can reduce the current for the same amount of power delivered. This is because:
P=V⋅I⟹I=PV
If V is increased, I decreases, leading to less power wasted in the cables.
2. Use Higher Resistance Cables: However, this is not practical as it would increase the power loss. The focus should be on increasing voltage.
Conclusion
To summarize, the power wasted in transmission cables is given by Pwasted=I2Rc. This wastage can be minimized by transmitting power at higher voltages, which reduces the current and consequently the power wasted in the transmission lines.
---
The power wasted in the transmission lines can be expressed using the formula:
Pwasted=I2Rc
where:
- Pwasted is the power wasted in the transmission cables,
- I is the current flowing through the cables,
- Rc is the resistance of the transmission cables.
The power delivered to the device can be calculated using the formula:
P=V⋅I
where:
- P is the total power delivered to the device,
- V is the voltage across the device,
- I is the current flowing through the device.
From the formula for power wasted, we can see that the power wasted is directly proportional to the square of the current (I2). This means that if the current increases, the power wasted in the transmission lines also increases significantly.
To reduce the power wasted in the transmission lines, we can either:
1. Increase the Voltage: By transmitting power at a higher voltage, we can reduce the current for the same amount of power delivered. This is because:
P=V⋅I⟹I=PV
If V is increased, I decreases, leading to less power wasted in the cables.
2. Use Higher Resistance Cables: However, this is not practical as it would increase the power loss. The focus should be on increasing voltage.
To summarize, the power wasted in transmission cables is given by Pwasted=I2Rc. This wastage can be minimized by transmitting power at higher voltages, which reduces the current and consequently the power wasted in the transmission lines.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NCERT EXEMPLAR ENGLISHChapter:CURRENT ELECTRICITYExercise:MCQs (More than one options)
Explore 5 Videos
- COMMUNICATION SYSTEMBook:NCERT EXEMPLAR ENGLISHChapter:COMMUNICATION SYSTEMExercise:LONG ANSWER TYPE QUESTIONS
Explore 5 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:NCERT EXEMPLAR ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTERExercise:LONG ANSWER TYPE QUESTION
Explore 5 Videos
Similar Questions
The voltage across a lamp, is 6.32V when the current passing through it is 3.4 A. Find the power consumed to appropriate significant figures.
View SolutionThe voltage across a lamp is 6.82 V when the current passing through it is 4.1 A. Find the power consumed to appropriate significant figures.
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionThe voltage across a lamp is (6.0±0.1)V and the current passing through it is (4.0±0.2) ampare. Find the power consumed by the lamp.
View SolutionA sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
View SolutionA sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
View SolutionThe resistance of each resisor in the circuit diagram shown in figure is the same and equal to R=1Ω The voltage across the terminals is U = 7V. Determine the current current i(Ampere) the jeads if their resistance can be neglected.
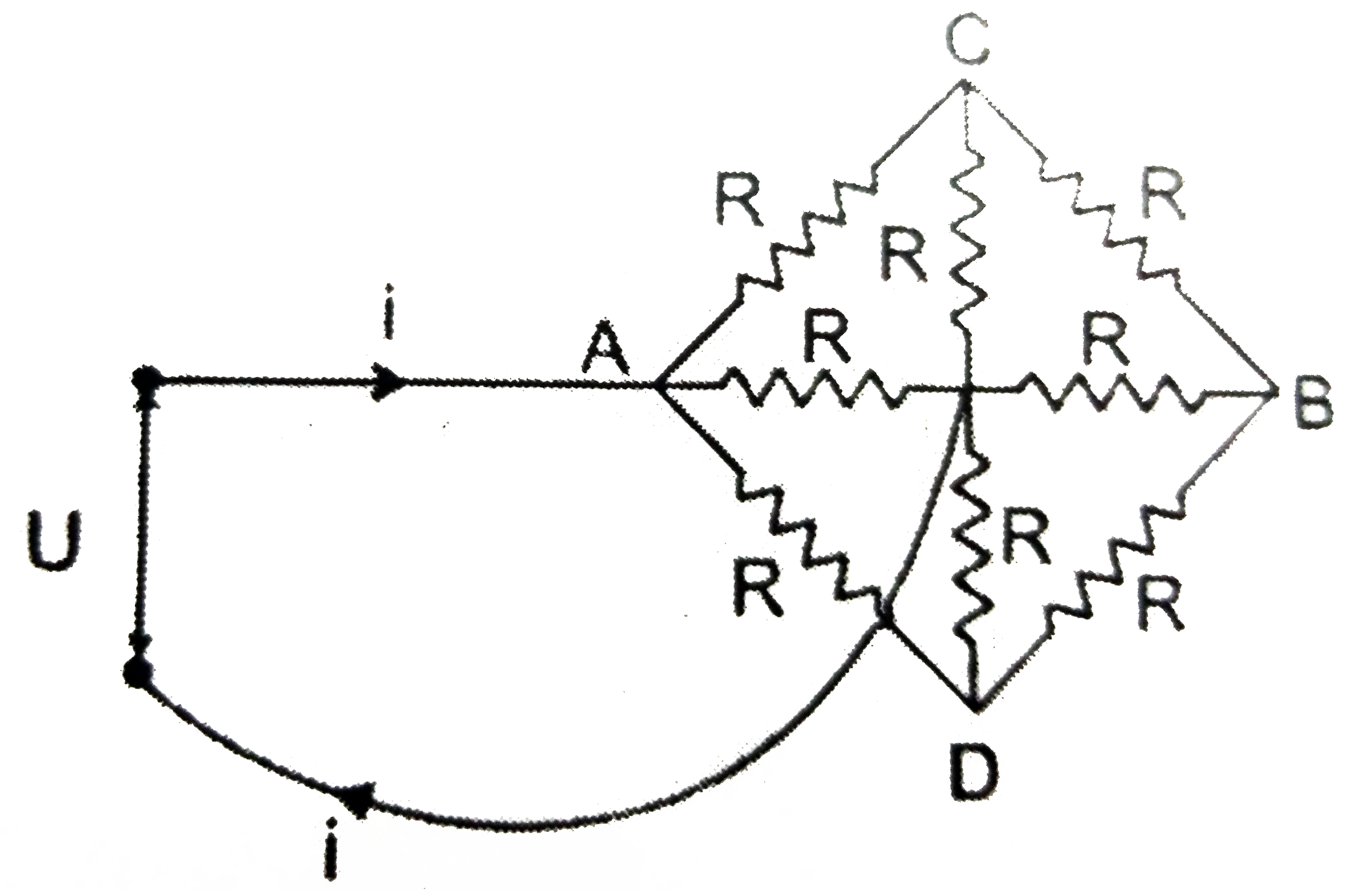
View SolutionAn element with emfε and interval resistance r is connected across an external resistance R. The maximum power in external circuit is 9W. The current flowing through the circuit in these conditions is 3A. Then which of the following is // are correct ?
View SolutionTwo identical batteries each of emf E=2 volt and internal resistance r=1 ohm are available t. produce heat in an external resistance by passing a current through it. What is the maximum power that can be developed across an external resistance R using these batteries?
View SolutionIn the given circuit, calculate -
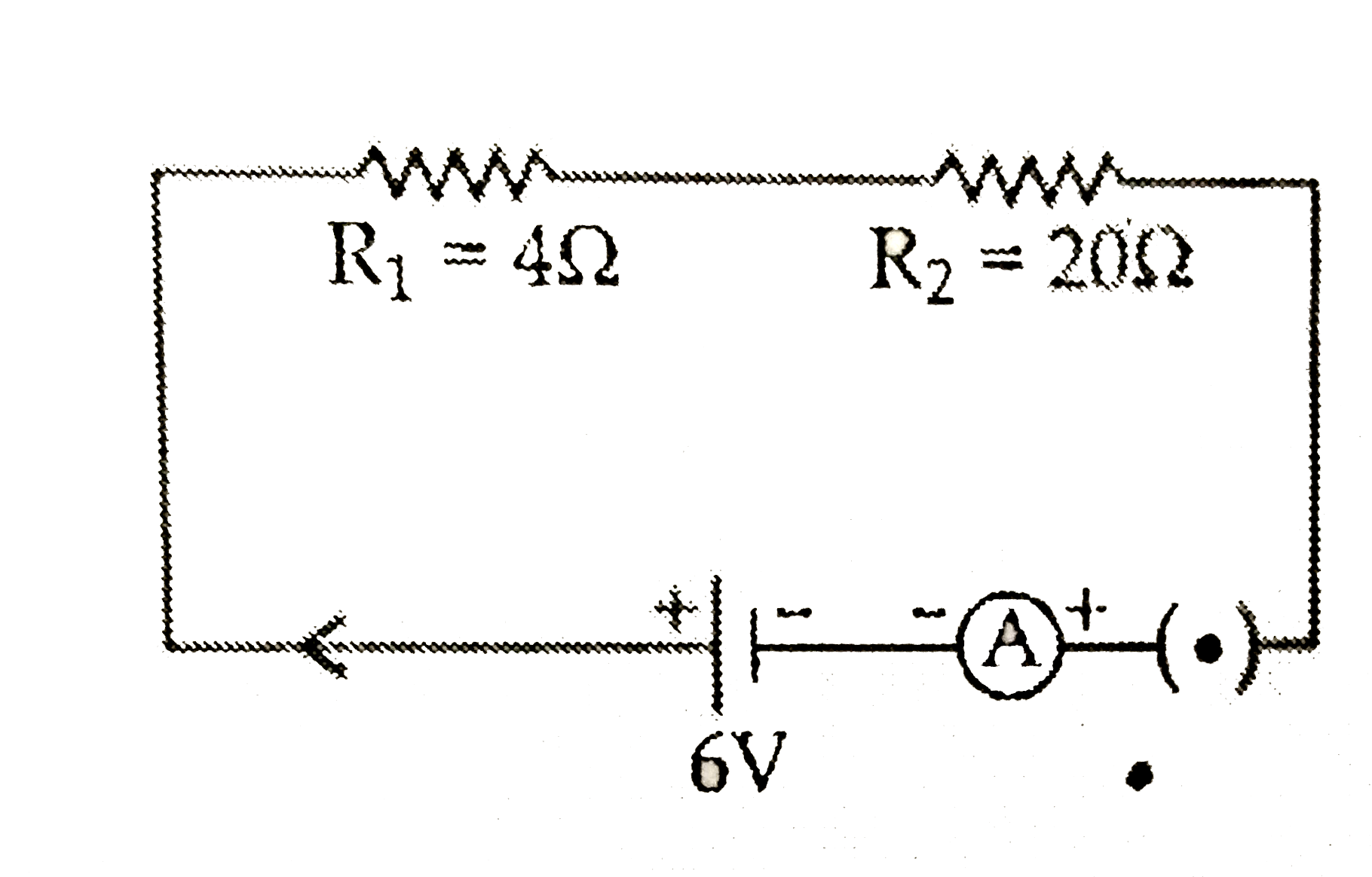
(a) the total resistance of the circuit,
(b) the current through the circuit, and
(c) the potential differences across R1andR2
View Solution

