A sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
Ip1Rcosθ
12I2pR
4πI2pR
1π2I2pR
The correct Answer is:B
To solve the problem, we need to find the power dissipated in a resistor when a sinusoidal AC current flows through it, given the peak current Ip.
1. Understand the relationship between peak current and RMS current:
The RMS (Root Mean Square) value of the current is related to the peak current Ip by the formula:
Irms=Ip√2
2. Calculate the average power dissipated in the resistor:
The power dissipated in a resistor when an AC current flows through it can be calculated using the formula:
P=I2rms⋅R
Substituting the expression for Irms:
P=(Ip√2)2⋅R
3. Simplify the expression:
Now, simplify the equation:
P=I2p2⋅R
4. Final expression for power:
Thus, the power dissipated in the resistor is given by:
P=12I2pR
Conclusion:
The power dissipated in the resistor when a sinusoidal AC current flows through it with a peak current Ip is:
P=12I2pR
The RMS (Root Mean Square) value of the current is related to the peak current Ip by the formula:
Irms=Ip√2
The power dissipated in a resistor when an AC current flows through it can be calculated using the formula:
P=I2rms⋅R
Substituting the expression for Irms:
P=(Ip√2)2⋅R
Now, simplify the equation:
P=I2p2⋅R
Thus, the power dissipated in the resistor is given by:
P=12I2pR
The power dissipated in the resistor when a sinusoidal AC current flows through it with a peak current Ip is:
P=12I2pR
Topper's Solved these Questions
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:Exercise -2 Part-1
Explore 14 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:Exercise -2 Part-2
Explore 6 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:HIGH LEVEL PROBLEMS
Explore 11 Videos
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Advanved level problems
Explore 17 Videos
Similar Questions
Knowledge Check
When a current I flows through a resistance R for time t, the electrical energy spent is :
AIRtBI2RtCIR2tDI2R/t
In an AC circuit with voltage V and current I, the power dissipated is
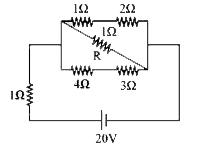
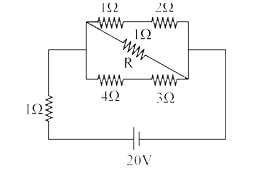
View SolutionCalculate the current flows through resistance 2Ω.
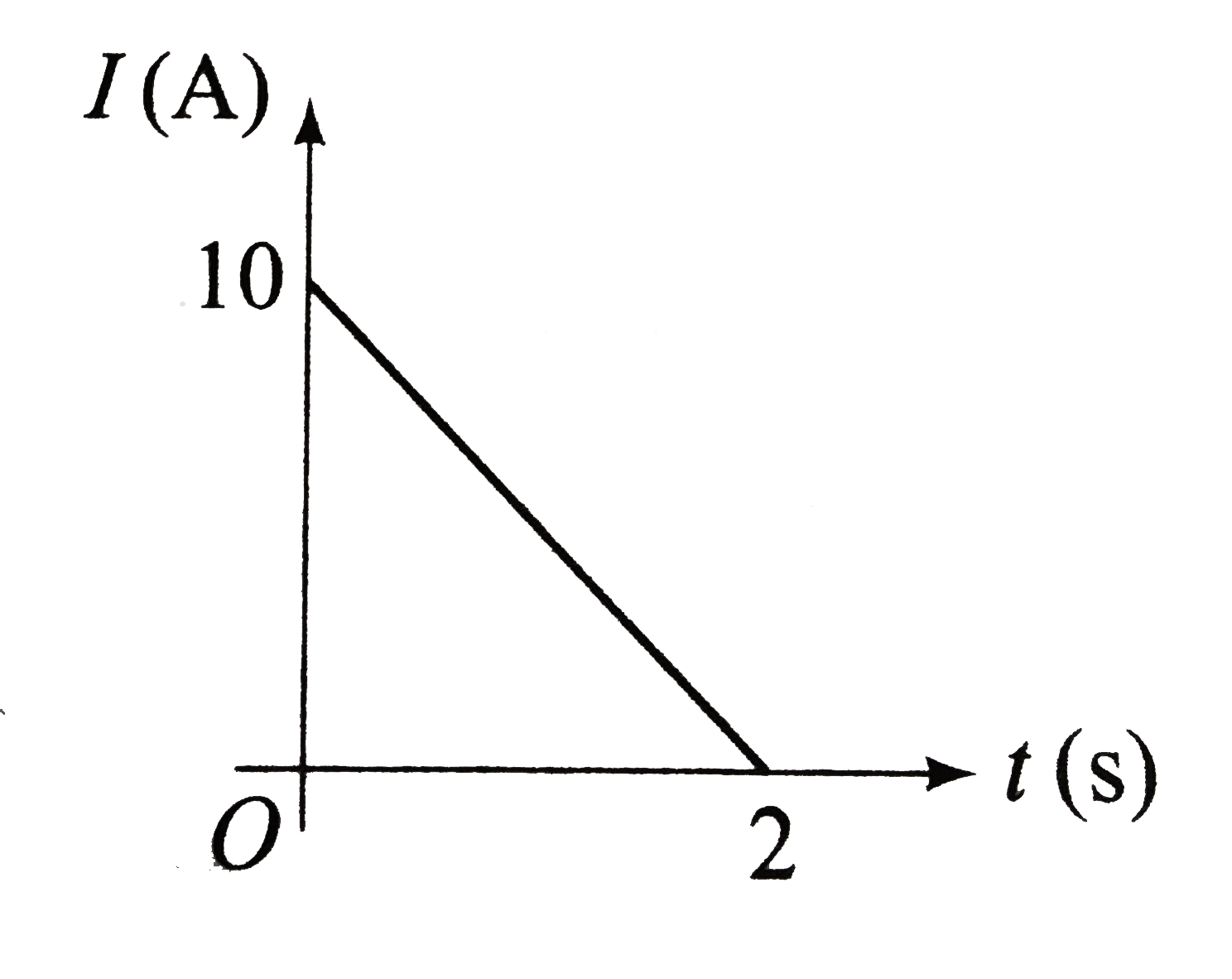
View SolutionA variable current flows through a 1Ω resistor for 2 s. Time dependence of the current is shown in the graph.
View SolutionA sinusoidal alternating current of peak value (I0) passes through a heater of resistance R. What is the mean power output of the heater?
View SolutionThe values of current (I) flowng through a given resistor of resistance (R ), for the corresponding values of potential difference (V) across the resistor are as given below :

Plot a graph between current (I) and potential difference (V) and determine the resistance (R ) of the resistor.
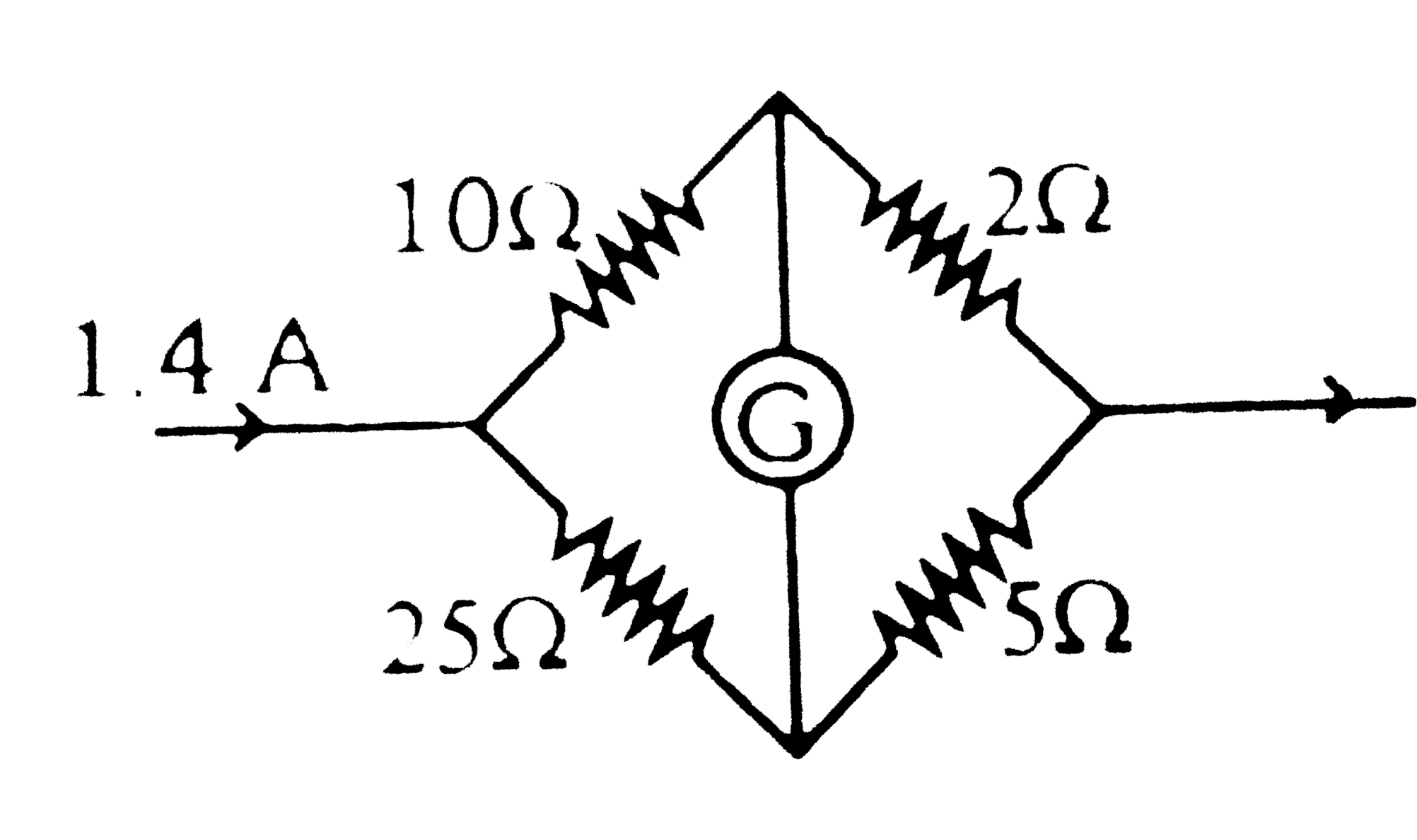
View SolutionIn the circuit, the current flowing through 10Ω resistance is
View SolutionIf the current I through a resistor is increased by 100% (assume that temperature remains unchanged), the increase in power dissipated will be :
View Solution