Find the ratio in which the line $3 x + 4 y + 2 = 0$ divides the distance between the lines $3 x + 4 y + 5 = 0 a n d 3 x = 4 y - 5 = 0 .$

A

$1 : 2$

B

$3 : 7$

C

$2 : 3$

D

$2 : 5$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let point A $(x_{1}, y_{1})$ lies on the line $3 x + 4 y + 5 = 0$ , then $3 x_{1} + 4 y_{1} + 5 = 0$

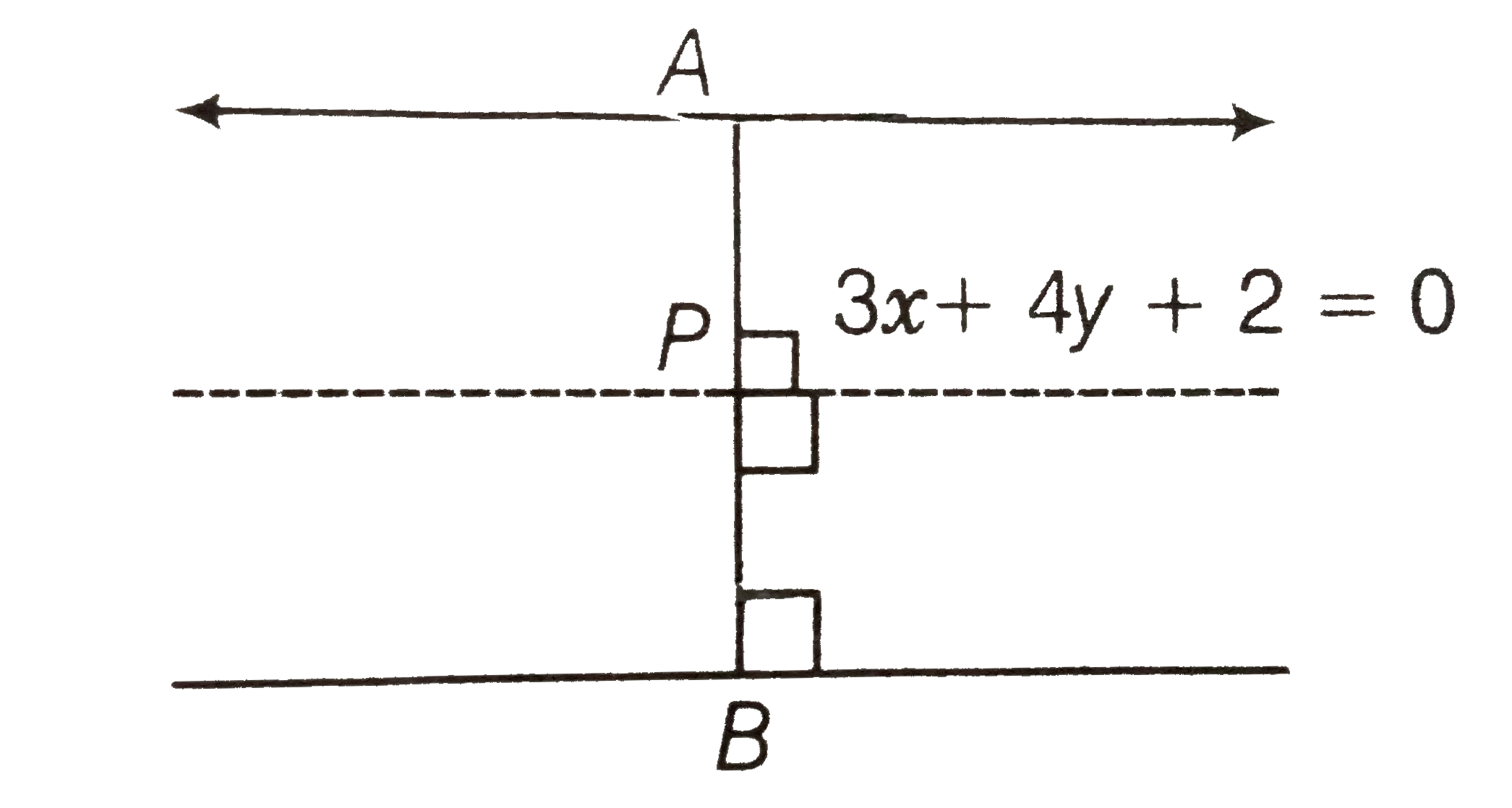
Now, perpendicular distance from A to the line
$3 x + 4 y + 2 = 0$
$\Rightarrow \frac{| 3 x_{1} + 4 y_{1} + 2 |}{\sqrt{9 + 16}} = \frac{| - 5 - 2 |}{\sqrt{9 + 16}} = \frac{- 7}{5}$
Let point $B (x_{2}, y_{2})$ lies on the ine $3 x + 4 y - 5 = 0$ i.e., $3 x_{2} + 4 y_{2} - 5 = 0$
Perpendicular distance form B to the line $3 x_{4} y + 2 = 0$ ,
$\frac{| 3 x_{2} + 4 y_{2} + 2 |}{\sqrt{9 + 16}} = \frac{| + 5 - 2 |}{\sqrt{9 + 16}} = \frac{3}{5}$
Hence, the required ratio is $\frac{3}{5} : \frac{7}{5}$ i.e., $3 : 7$ .

Updated on:21/07/2023

|

Class 11 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

The ratio in which the line $3 x + 4 y + 2 = 0$ divides the distance between the lines $3 x + 4 y + 5 = 0$ and $3 x + 4 y - 5 = 0$
A $1 : 2$
B $3 : 7$
C $2 : 3$
D $2 : 5$
Distance between the lines $3 x + 4 y - 5 = 0$ and $6 x + 8 y - 45 = 0$ is
A $\frac{1}{3}$
B $\frac{7}{2}$
C1
D $\frac{2}{7}$

NCERT EXEMPLAR ENGLISH-STRAIGHT LINES-Objective type questions

Home
Ask Doubt
Profile