A circle of radius 3 cm can be drawn through two points A, B such that AB=6 cm. State true or false
The correct Answer is:1
To determine whether a circle of radius 3 cm can be drawn through two points A and B such that the distance AB is 6 cm, we can follow these steps:
1. Understand the Given Information:
- The radius of the circle (r) is given as 3 cm.
- The distance between points A and B (AB) is given as 6 cm.
2. Identify the Relationship Between Diameter and Radius:
- The diameter (d) of a circle is twice the radius. Therefore, we can express this relationship as:
d=2×r
3. Calculate the Diameter Using the Given Radius:
- Substitute the radius into the diameter formula:
d=2×3 cm=6 cm
4. Compare the Diameter with the Length of AB:
- We see that the calculated diameter (6 cm) is equal to the distance AB (6 cm).
5. Conclusion:
- Since the distance AB is equal to the diameter of the circle, it confirms that points A and B can indeed lie on a circle with a radius of 3 cm. Thus, a circle can be drawn through points A and B with the given conditions.
Final Answer:
The statement is True.
---
- The radius of the circle (r) is given as 3 cm.
- The distance between points A and B (AB) is given as 6 cm.
- The diameter (d) of a circle is twice the radius. Therefore, we can express this relationship as:
d=2×r
- Substitute the radius into the diameter formula:
d=2×3 cm=6 cm
- We see that the calculated diameter (6 cm) is equal to the distance AB (6 cm).
- Since the distance AB is equal to the diameter of the circle, it confirms that points A and B can indeed lie on a circle with a radius of 3 cm. Thus, a circle can be drawn through points A and B with the given conditions.
The statement is True.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.3
20 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
In quadrilateral ABCD angled D=90∘, BC=38cm and DC=25cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB=27cm. Find the radius of the circle.
A28cmB14cmC35cmD19cmDraw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and find the length of each tangent.
A4cmB6cmC2cmD7cm
Using ruler and compasses only: draw a circle of radius 4cm. Produce AB, a diameter of this circle, upto point X so that BX= 4cm. Construct a circle to touch AB at X and to touch the circle, drawn earlier, externally.
View SolutionIn Figure 6, three circles each of radius 3-5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region).
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
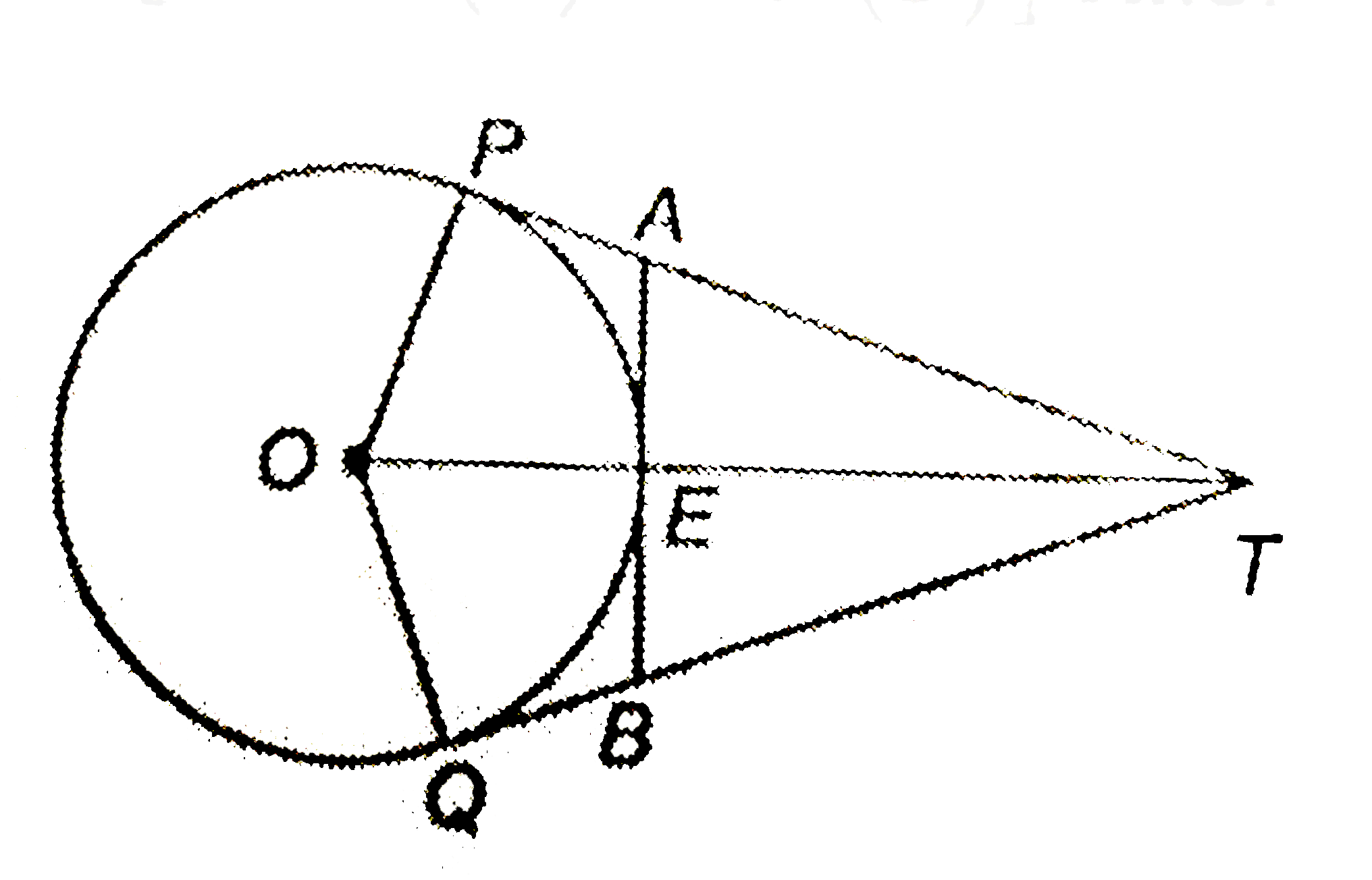
View SolutionType V: O is the center of the circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E . If AB is the tangent to the circle at E; find the length of AB.
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find length of AB.
View SolutionDraw a circle of radius 3 cm and take a point P outside it. Without using the centre of the circle draw two tangents of the circle from the point P.
View Solution
