Two chords AB and AC of a circle with centre O are on the opposite sides of OA. Then, ∠OAB=∠OAC.
To determine whether the statement "Two chords AB and AC of a circle with center O are on the opposite sides of OA, then angle OAB = angle OAC" is true or false, we can analyze the situation step by step.
1. Draw the Circle:
- Start by drawing a circle with center O.
2. Identify the Chords:
- Draw two chords AB and AC such that they are on opposite sides of the line segment OA.
3. Label the Points:
- Label the points where the chords intersect the circle as A, B, and C.
4. Identify the Angles:
- We need to analyze the angles ∠OAB and ∠OAC.
5. Use Properties of the Circle:
- Since AB and AC are chords of the circle, we know that OB and OC are radii of the circle. Therefore, OB = OC.
6. Common Side:
- The line segment OA is common to both triangles OAB and OAC.
7. Triangles OAB and OAC:
- Now we have two triangles: OAB and OAC.
- We know that OB = OC (radii of the circle) and OA is common to both triangles.
8. Check for Congruence:
- For the triangles OAB and OAC to be congruent, we would need to show that all three sides are equal or that they have a sufficient number of equal angles and sides.
- However, we cannot conclude that AB = AC just from the information given.
9. Conclusion:
- Since the triangles OAB and OAC are not congruent (as we cannot establish that AB = AC), we cannot say that ∠OAB = ∠OAC.
- Therefore, the statement is false.
Final Answer:
The statement "Two chords AB and AC of a circle with center O are on the opposite sides of OA, then angle OAB = angle OAC" is false.
- Start by drawing a circle with center O.
- Draw two chords AB and AC such that they are on opposite sides of the line segment OA.
- Label the points where the chords intersect the circle as A, B, and C.
- We need to analyze the angles ∠OAB and ∠OAC.
- Since AB and AC are chords of the circle, we know that OB and OC are radii of the circle. Therefore, OB = OC.
- The line segment OA is common to both triangles OAB and OAC.
- Now we have two triangles: OAB and OAC.
- We know that OB = OC (radii of the circle) and OA is common to both triangles.
- For the triangles OAB and OAC to be congruent, we would need to show that all three sides are equal or that they have a sufficient number of equal angles and sides.
- However, we cannot conclude that AB = AC just from the information given.
- Since the triangles OAB and OAC are not congruent (as we cannot establish that AB = AC), we cannot say that ∠OAB = ∠OAC.
- Therefore, the statement is false.
The statement "Two chords AB and AC of a circle with center O are on the opposite sides of OA, then angle OAB = angle OAC" is false.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.3
20 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
If two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC, prove that AB=AC , i.e. the chords are equal.
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
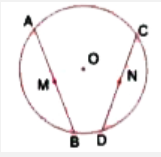
∠AMN=∠CNM.
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :

(i) ∠BMN=∠DNM
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionChords AB and CD of a circle with centre O, intersect at a point E. If OE bisects angle AED, prove that chord AB = chord CD.
View SolutionTwo chords AB and CD of a circle are each at distances 4 cm from the centre. Then,
View SolutionChords AB and CD of a circle are parallel to each other and lie on opposite sides of the centre of the circle. If AB = 36 cm, CD = 48 cm and the distance between the chords is 42 cm, find the radius of the circle.
View SolutionThe length of two parallel chords of a circle are 6 cm and 8 cm . The radius of the circle is 5 cm. Find the distance btween them if :
(i) chords are on the same side of the centre.
(ii) chords are on the opposite side of the centre.
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
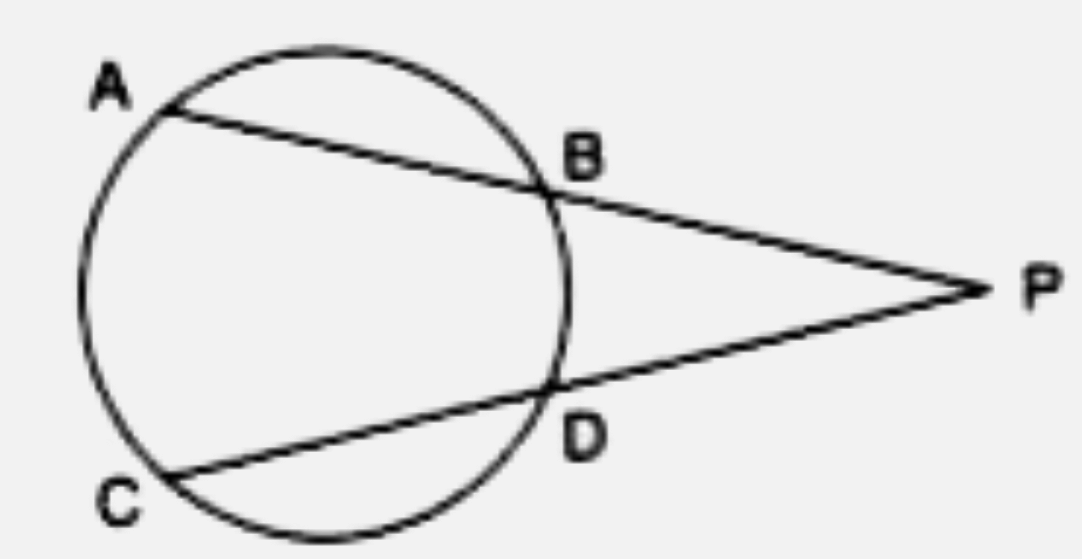
PB=PD
View Solution
