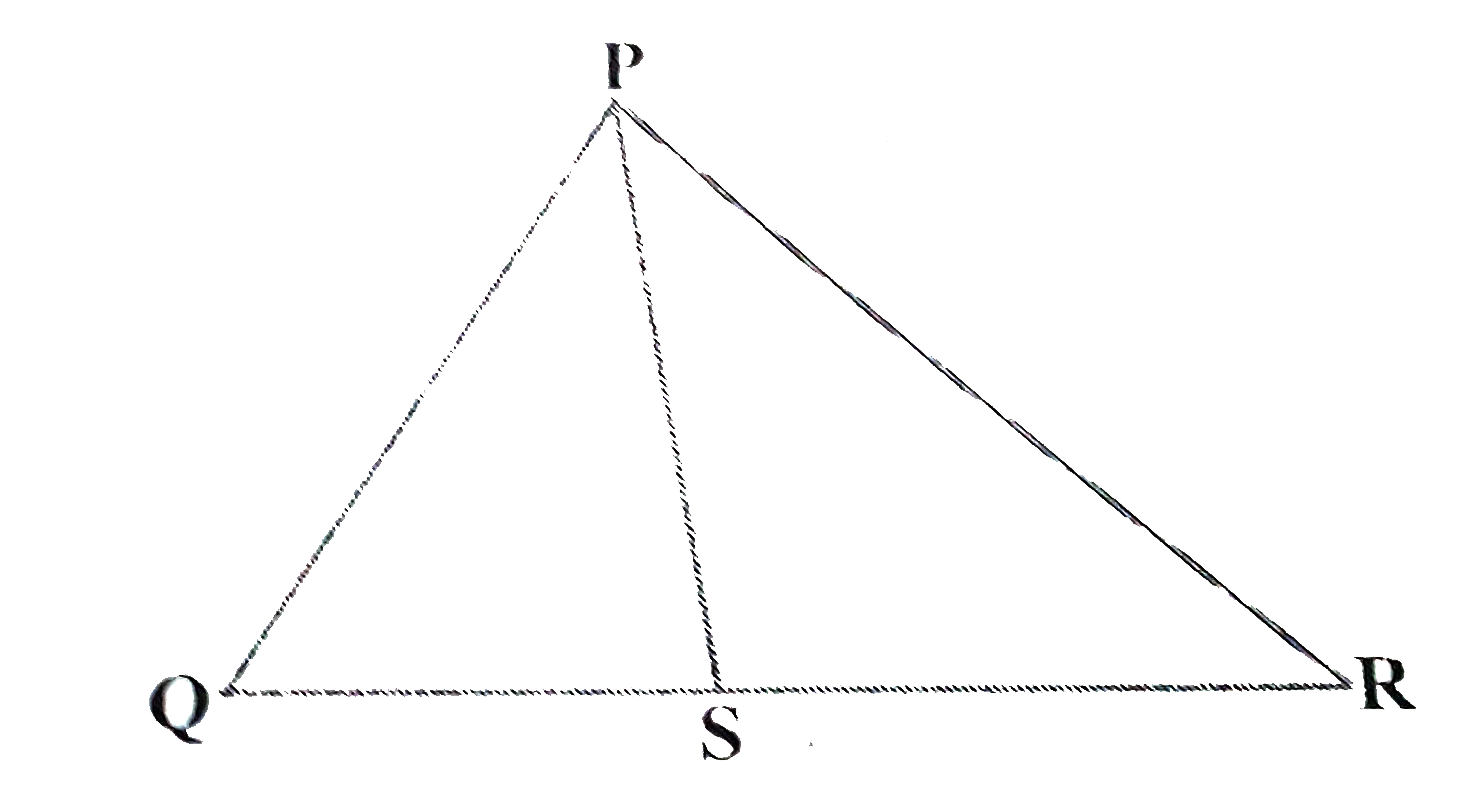
If PS is the bisector of ∠QPR and PT⊥QR . Show that ∠TPS=12(∠Q−∠R).
Given In ΔPQR,∠>∠R, PA is the bisector of ∠QPRandPM⊥ QR .
To prove ∠APM=12(∠Q−∠R)
Proof Since, PA is the bisector of ∠QPR
∴ ∠QPA=∠APR ....(i)
In ΔPQM, ∠PQM+∠PMQ+∠QPM+180∘ [by angle sum property of a triangle]
⇒ ∠PQM+90∘+∠QPM=180∘ [∵PM⊥QR⇒∠PMQ=90∘]
⇒ ∠PQM+90∘−∠QPM ...(ii)
In ΔPMR, ∠PMR+∠PRM+∠RPM=180∘ [by angles sum property of a triangles]
⇒ ∠90∘+∠PRM+∠RPM=180∘ [∵PM⊥QR⇒∠PMQ=90∘]
⇒ ∠PRM=180∘−90∘−∠RPM
⇒ ∠PRM=90∘−∠RPM ...(iii)
On subtracting Eq. (iii) from Eq. (ii), we get
∠Q−∠R=(90∘−∠QPM)−(90∘−∠RPM) [where∠PQM=∠Qand∠PRM=∠R]
⇒ ∠Q−∠R=∠RPM−∠QPM
⇒ ∠Q−∠R=[∠APM+∠APM]−[∠QPA−∠APM] ...(iv)
⇒ ∠Q−∠R=∠QPA+∠APM−∠QPA−∠APM [by using Eq. (i)]
⇒ ∠Q−∠R=2∠APM
∴ ∠APM=12(∠Q−∠R) Hence proved.
Topper's Solved these Questions
Similar Questions
In figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.
View SolutionIn Fig. , the side QR of △ PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.
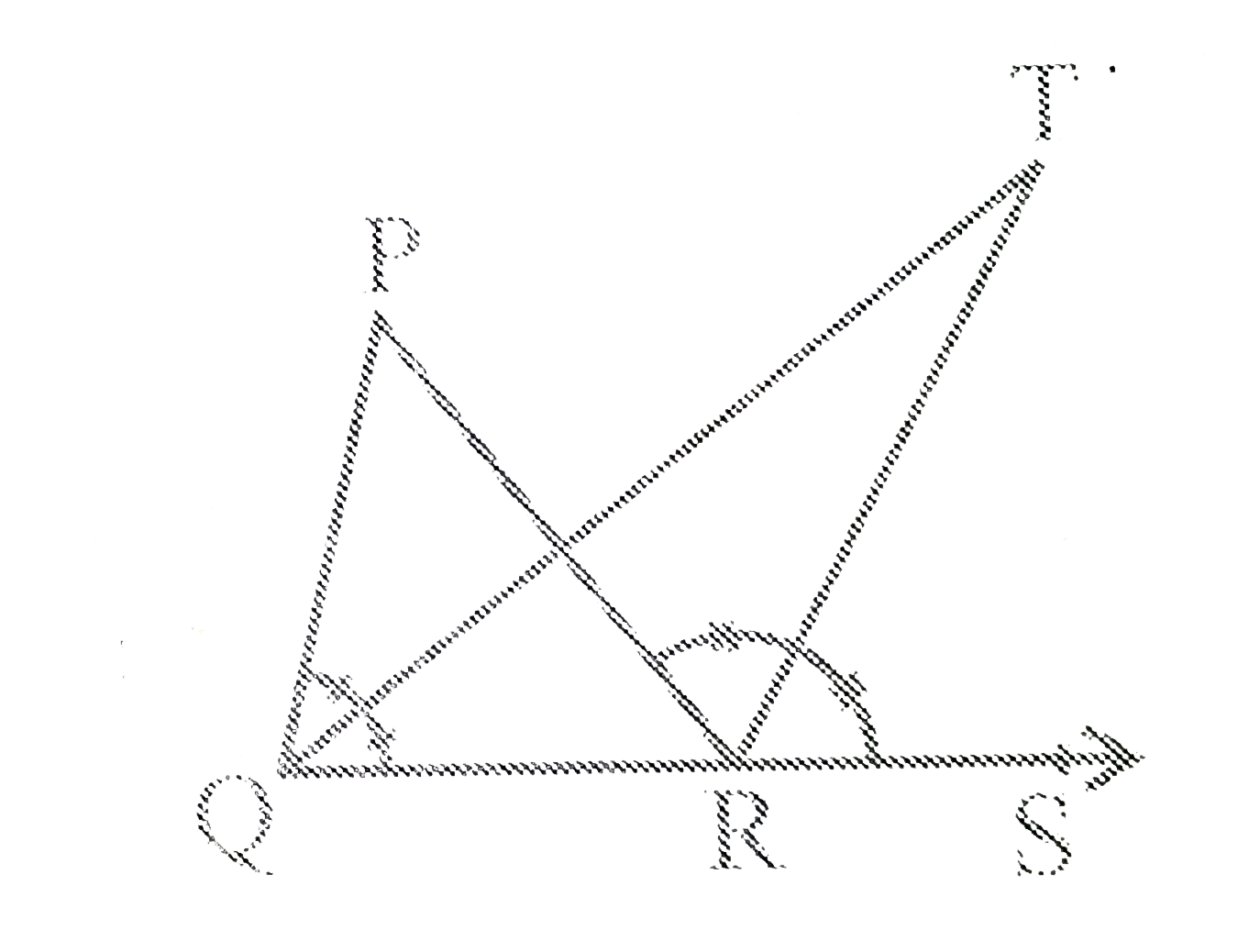
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR\ and∠PRS meet at point T, then prove that ∠QTR=12∠QPR .
View SolutionIn Figure, PQ>PR.QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ>SR.
View SolutionIn figure, PQ=PR . Show that PS>PQ.
View SolutionIn ABC,D is the mid-point of AB,P is any point of BC.CQPD meets AB in Q . Show that ar(BPQ)=12ar(ABC).
View SolutionIn PQR , S is any point on the side QR . Show that PQ+QR+RP>2PS
View SolutionIf P + Q = R and P - Q = S, prove that R2+S2=2(P2+Q2)
View SolutionIn Figure, ∠PQR= ∠PRQ, then prove that ∠PQS= ∠PRT.
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.

View Solution

