In Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of meet at point T, then prove that .
To prove that ∠QTR=12∠QPR, we will follow these steps:
Step 1: Identify the Angles
Let:
- ∠PQR=∠4
- ∠QPR=∠2
- ∠PRS=∠6
- ∠QTR=∠1
- ∠PRT=∠5
Step 2: Use the Angle Bisector Property
Since QT is the bisector of ∠PQR, we have:
∠PQT=∠QTR=∠1
Thus, we can say:
∠PQT=∠3=∠1
And since TR is the bisector of ∠PRS, we have:
∠PRT=∠5=12∠PRS=12∠6
Step 3: Apply the Exterior Angle Theorem
In triangle PQR:
∠PRS=∠PQR+∠QPR
This gives us:
∠6=∠4+∠2
In triangle QTR:
∠PRT=∠QTR+∠PQT
This gives us:
∠5=∠1+∠3
Step 4: Relate the Angles
From the angle bisector property, we have:
∠5=12∠6
Substituting ∠6 from the previous step:
∠5=12(∠4+∠2)
Step 5: Equate the Two Expressions for ∠5
Now we have two expressions for ∠5:
1. ∠5=∠1+∠3
2. ∠5=12(∠4+∠2)
Setting these equal gives us:
∠1+∠3=12(∠4+∠2)
Step 6: Substitute and Simplify
From the angle bisector property, we know:
∠3=∠1
Substituting this into the equation:
∠1+∠1=12(∠4+∠2)
This simplifies to:
2∠1=12(∠4+∠2)
Step 7: Solve for ∠1
Multiplying both sides by 2:
4∠1=∠4+∠2
Thus:
∠1=12∠2
Conclusion
Therefore, we have proved that:
∠QTR=12∠QPR
Let:
- ∠PQR=∠4
- ∠QPR=∠2
- ∠PRS=∠6
- ∠QTR=∠1
- ∠PRT=∠5
Since QT is the bisector of ∠PQR, we have:
∠PQT=∠QTR=∠1
Thus, we can say:
∠PQT=∠3=∠1
And since TR is the bisector of ∠PRS, we have:
∠PRT=∠5=12∠PRS=12∠6
In triangle PQR:
∠PRS=∠PQR+∠QPR
This gives us:
∠6=∠4+∠2
∠PRT=∠QTR+∠PQT
This gives us:
∠5=∠1+∠3
From the angle bisector property, we have:
∠5=12∠6
Substituting ∠6 from the previous step:
∠5=12(∠4+∠2)
Now we have two expressions for ∠5:
1. ∠5=∠1+∠3
2. ∠5=12(∠4+∠2)
∠1+∠3=12(∠4+∠2)
From the angle bisector property, we know:
∠3=∠1
Substituting this into the equation:
∠1+∠1=12(∠4+∠2)
This simplifies to:
2∠1=12(∠4+∠2)
Multiplying both sides by 2:
4∠1=∠4+∠2
Thus:
∠1=12∠2
Therefore, we have proved that:
∠QTR=12∠QPR
Topper's Solved these Questions
- LINES AND ANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINES AND ANGLESExercise:Exercise 6 A
Explore 19 Videos
- LINES AND ANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINES AND ANGLESExercise:Exercise 6 B
Explore 16 Videos
- LINES AND ANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINES AND ANGLESExercise:Revision Exercise (long Answer Questions )
Explore 6 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Revision Exercise
Explore 12 Videos
- NUMBER SYSTEMBook:NAGEEN PRAKASHAN ENGLISHChapter:NUMBER SYSTEMExercise:Revision Exercise (short Answer Questions)
Explore 10 Videos
Similar Questions
In Fig. , the side QR of △ PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.
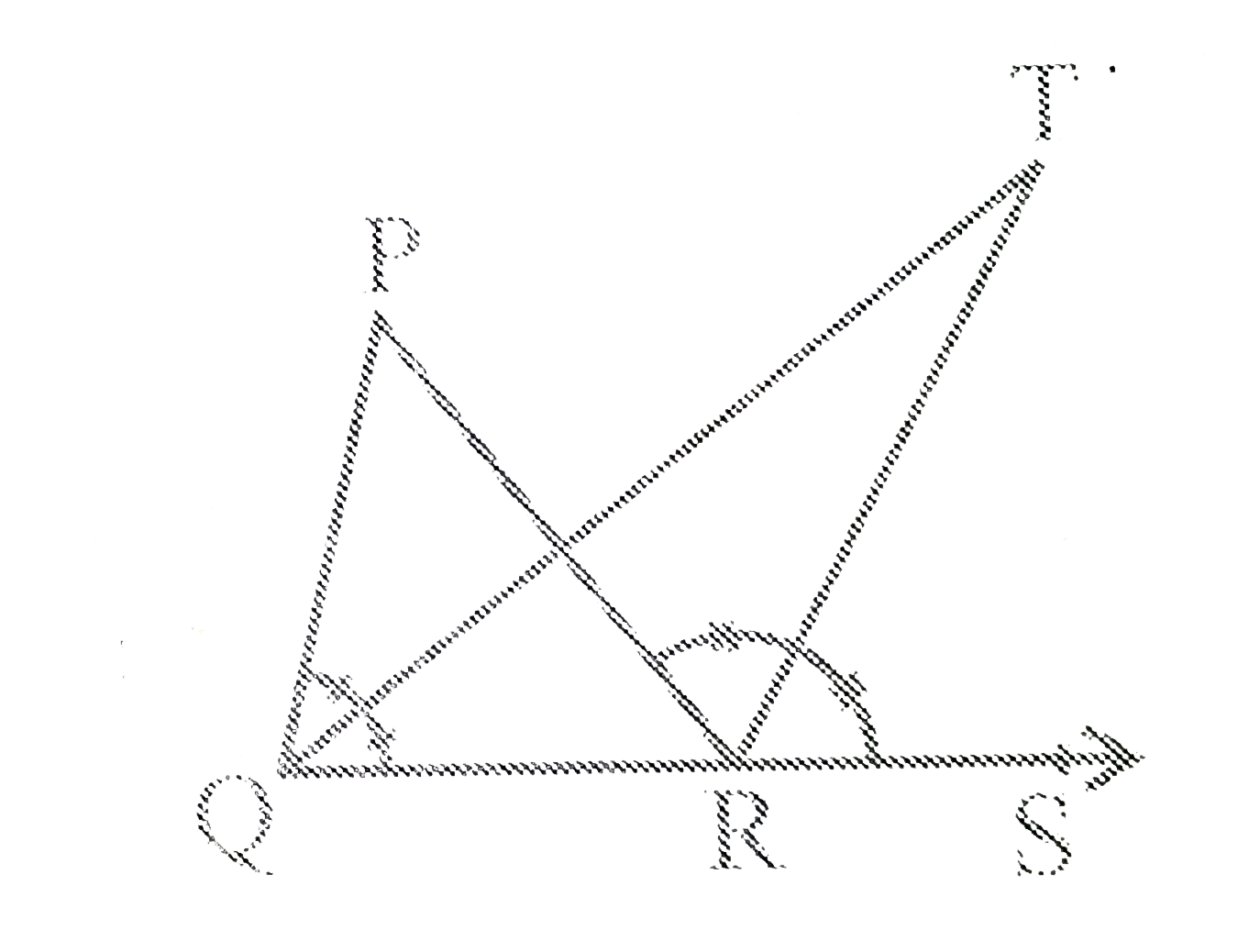
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
View SolutionIn Figure, ∠PQR= ∠PRQ, then prove that ∠PQS= ∠PRT.
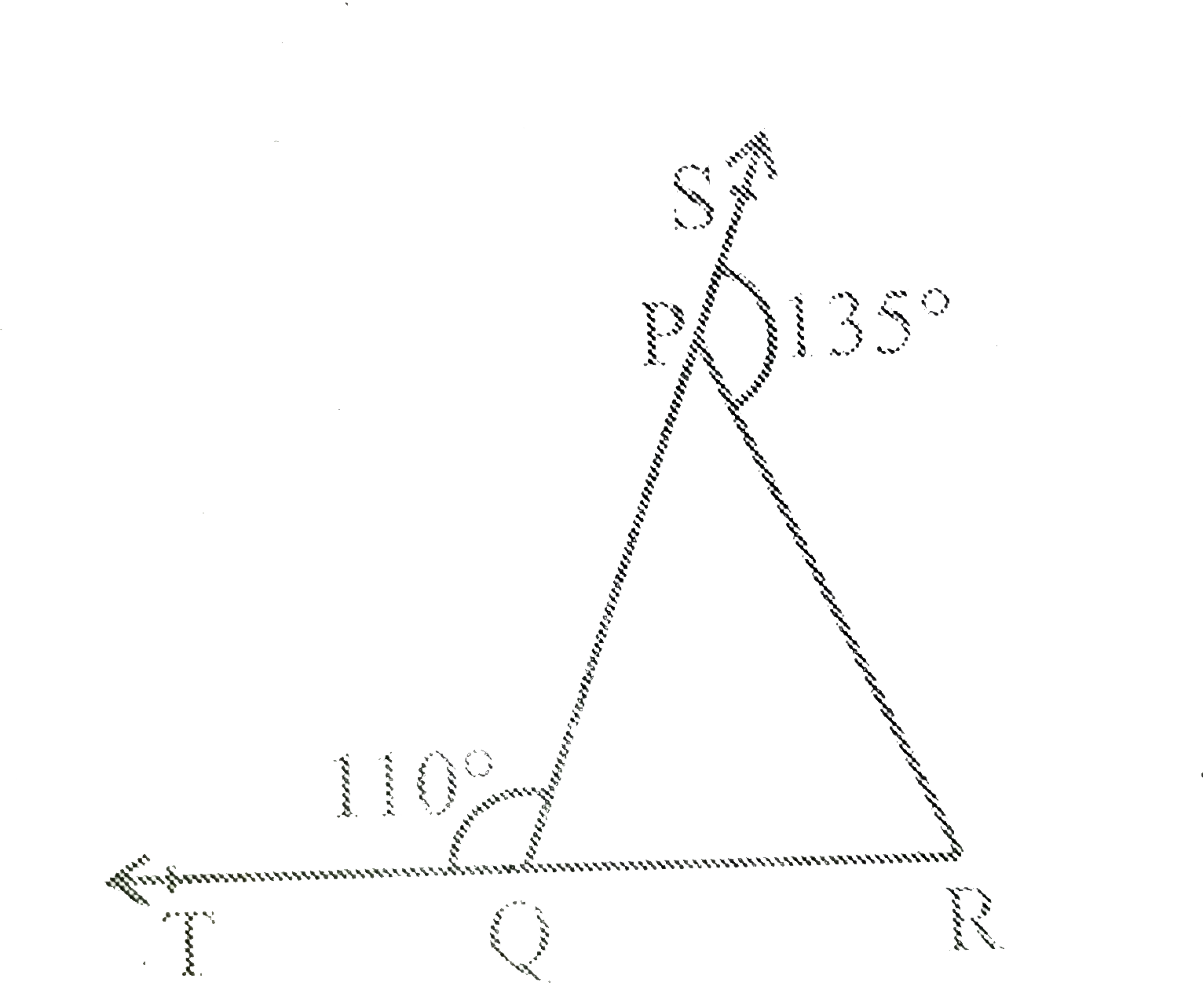
View SolutionIn Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
View SolutionIn Figure, PQ>PR.QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ>SR.
View Solutionsides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ.
View SolutionIn Figure, side QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350and ∠PQT=110∘, find ∠PRQ
View SolutionIn figure, sides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ. Figure
View SolutionIn figure, sides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ. Figure
View SolutionIf PS is the bisector of ∠QPR and PT⊥QR . Show that ∠TPS=12(∠Q−∠R).
View Solution