In the adjoining figure , we have X and Y are the mid - point of AC and BC and AX = CY . Show that AC =BC.
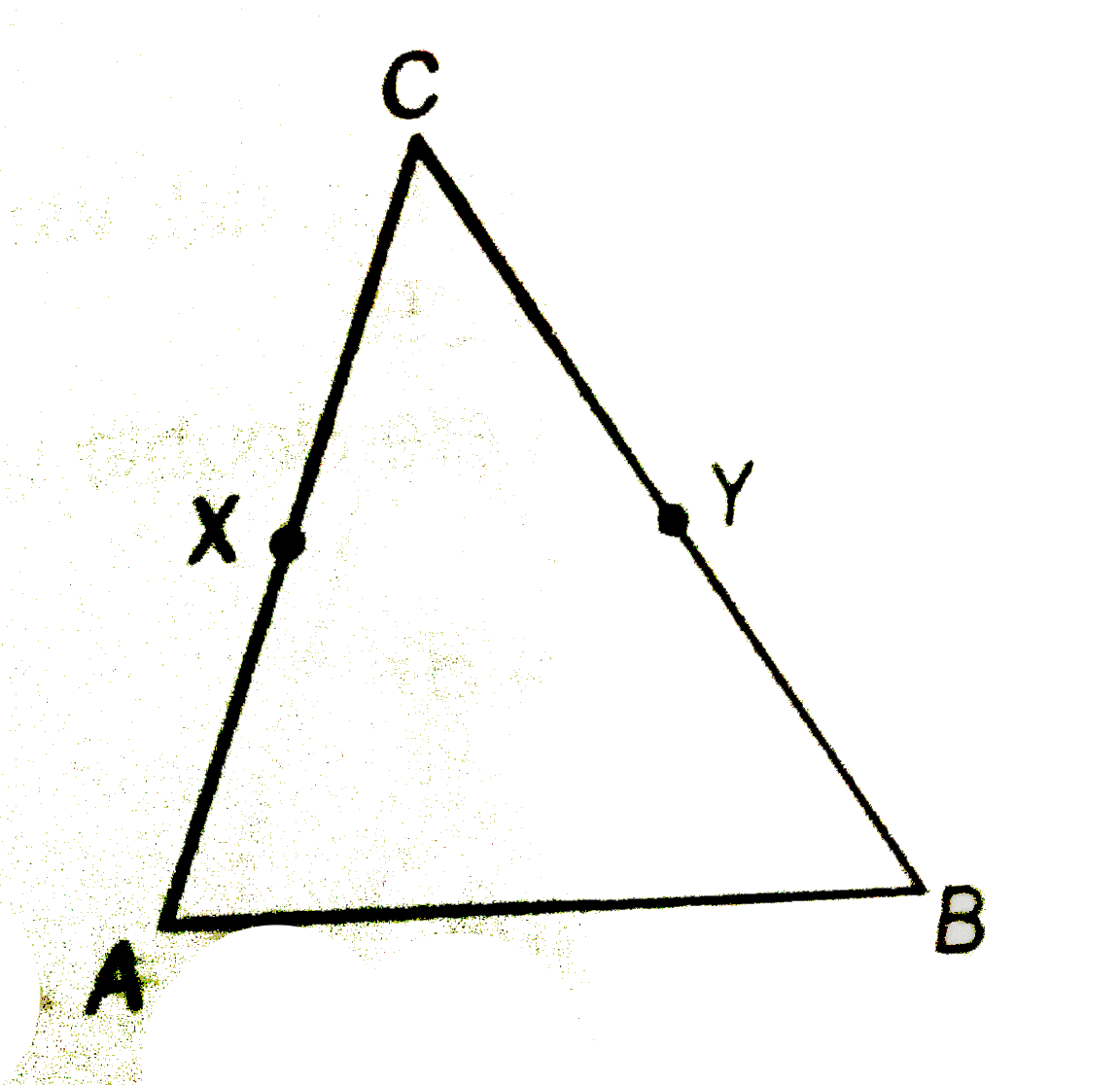
Given , X is the mid - point of AC.
∴AX=CX=12AC
⇒ 2AX=2CX=AC ...(i)
and Y is the mid -point of BC.
∴BY=CY=12BC
⇒ 2BY=2CY=BC ...(ii)
Also, given AX=CY ...(iii)
According to Euclid's axiom, things which are double of the same things are equal to one another.
From Eq. (iii), 2AX=2CY
⇒ AC=BC ["from Eqs. ("i) and (ii)"]
Topper's Solved these Questions
- INTRODUCTION TO EUCLID GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO EUCLID GEOMETRYEXERCISE - Exercise 5.4 Long Answer Type Questions
5 Videos
- INTRODUCTION TO EUCLID GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO EUCLID GEOMETRYEXERCISE - Exercise 5.2 Very Short Answer Type Questions
9 Videos
- HERON'S FORMULABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - HERON'S FORMULAEXERCISE - Long Answer Type Questions
8 Videos
- LINEAR EQUATION IN TWO VARIABLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR EQUATION IN TWO VARIABLESEXERCISE - Exercise 4.8
1 Videos
Similar Questions
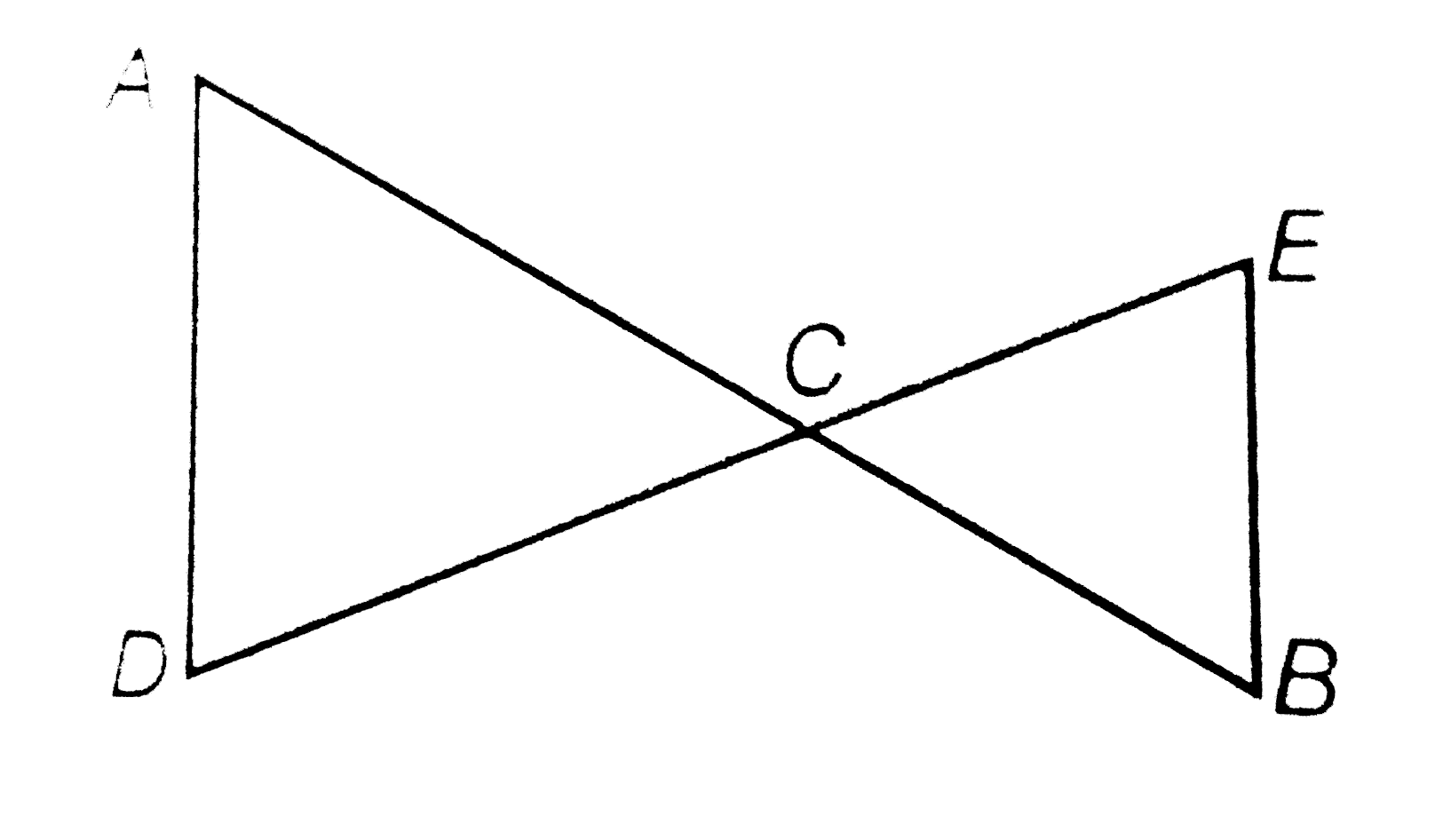
In the adjoining figure , we have AC=DC and CB = CE. Show that AB=DE.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

View SolutionIn the adjoining figure
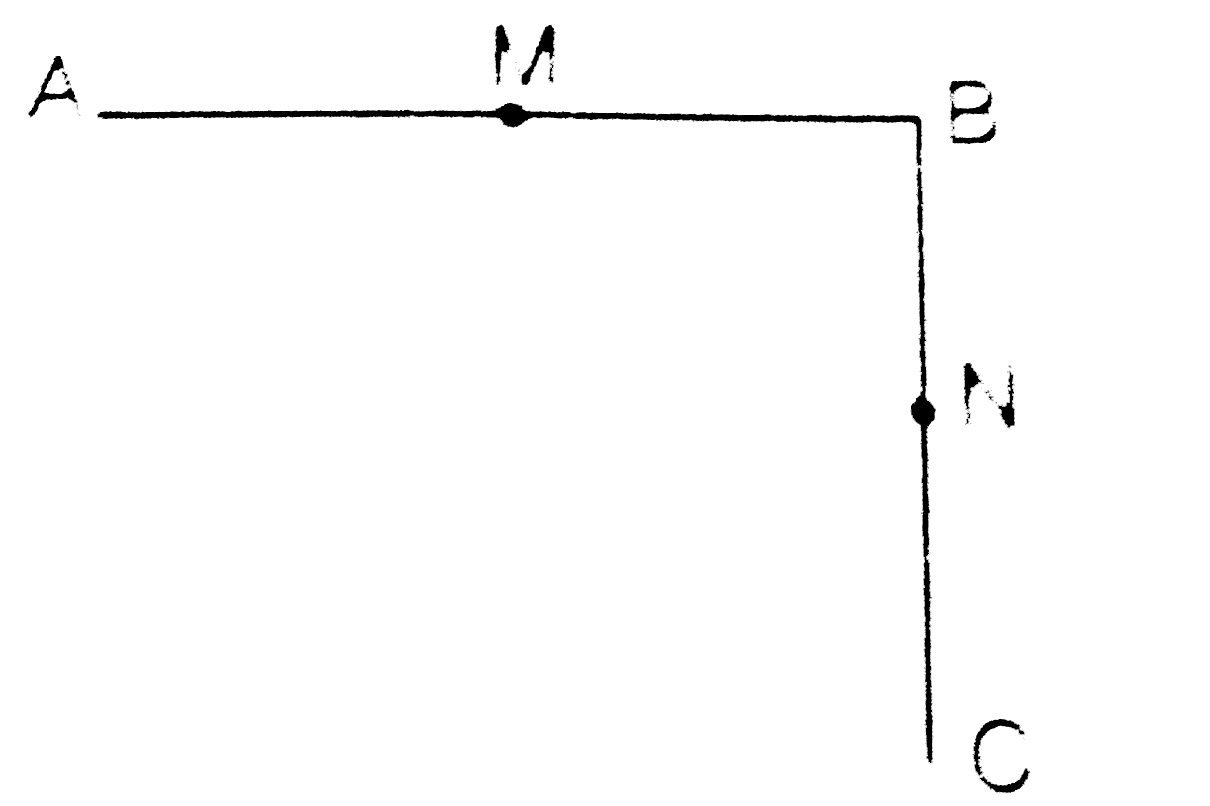
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.
View SolutionIn the figure, given below X and Y are the mid-points of AB and AC respectively. Given that BC = 6 cm, AB = 5-4 cm and AC = 5-0 cm, calculate the perimeter of trapezium YXBC.

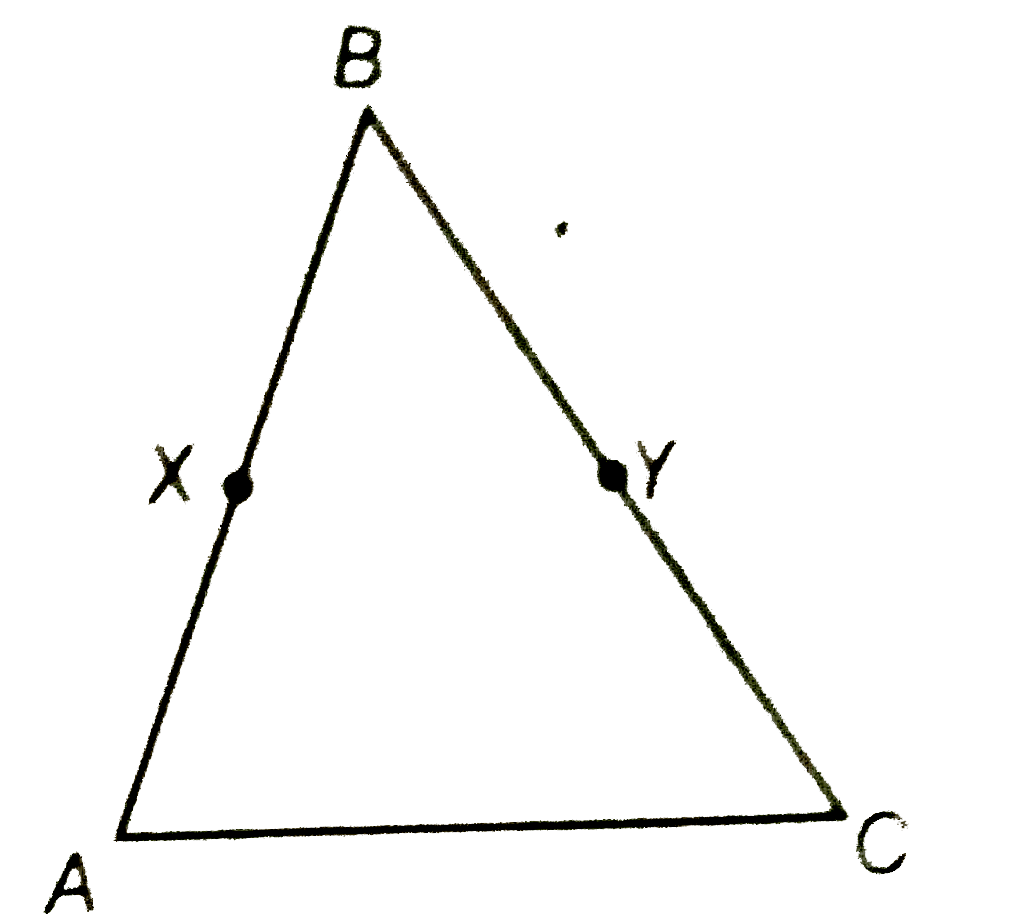
View SolutionIn the adjoining figure, if AB = BC and BX =BY, then show that AX=CY
View SolutionIn the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that : EF = AC.
View SolutionIn theadjoining figure, ∠DAB=∠ABC and AD=BC prove that BD=AC.

View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.

View SolutionIn the adjoining figure, O is the centre of a circle in which AB and CD are two diameters. Prove that AC| |BD and AD| |BC. If ∠OBD=50∘, then find the value of ∠AOC.

View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC<AB+AC.
View Solution
