In the ajoining figure , we have∠ABC=∠ACBand∠3=∠4. Show that BD=DC.
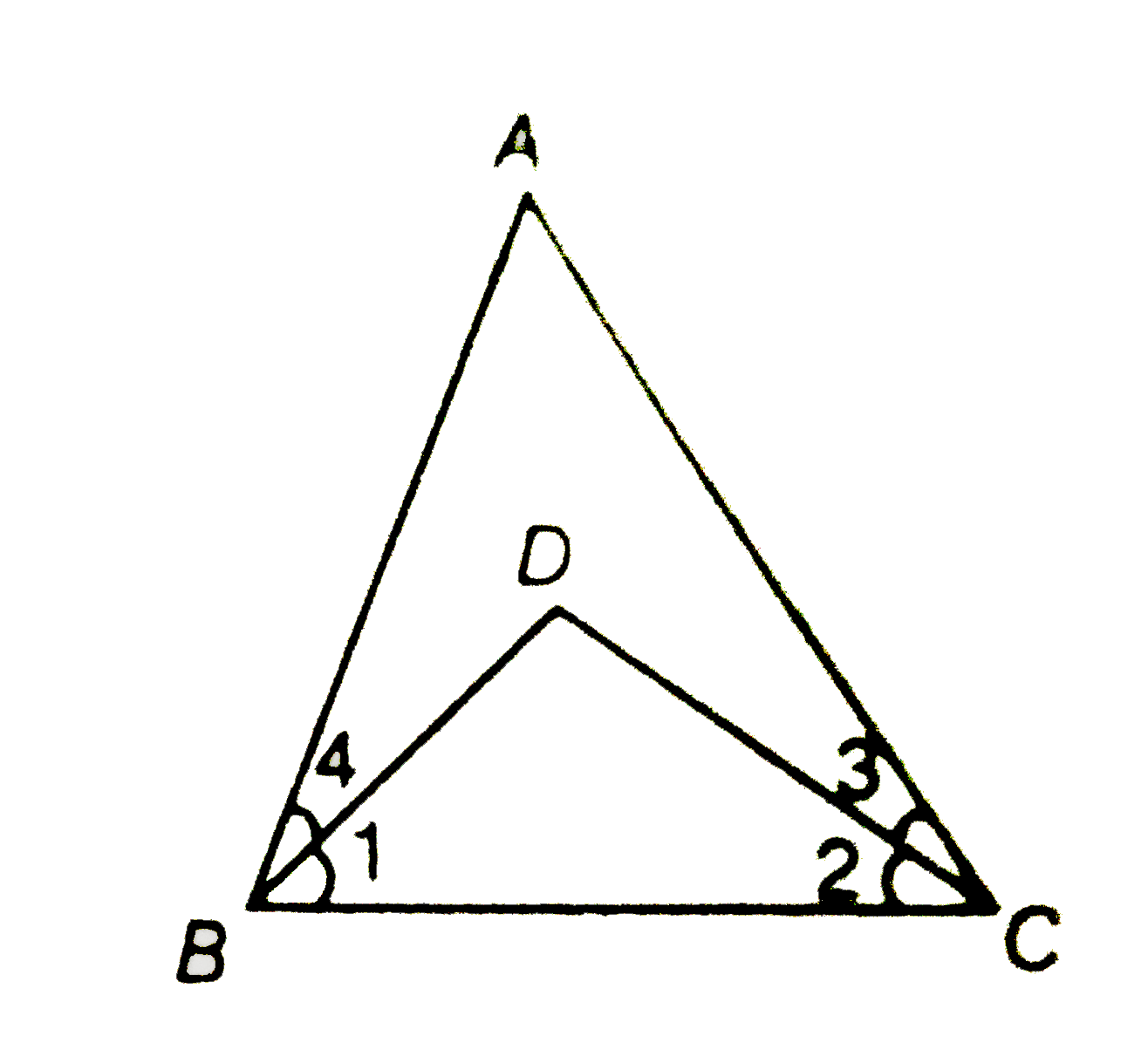
Given , ∠ABC=∠ACB ... (i)
and ∠4=∠3 ...(ii)
According to Eulid's axiom , if equals are subtracted from equals, then remainders are also equal. On subtracting Eq. (ii) From Eq.(i) we get
∠ABC−∠4=∠ACB−∠3
⇒∠1=∠2
Now , in ΔBDC,∠1=∠2
⇒ DC =BD [sides opposite to equales are equal]
∴ BD=DC.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO EUCLID GEOMETRYEXERCISE - Exercise 5.4 Long Answer Type Questions5videos
INTRODUCTION TO EUCLID GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO EUCLID GEOMETRYEXERCISE - Exercise 5.2 Very Short Answer Type Questions9videos
INTRODUCTION TO EUCLID GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - HERON'S FORMULAEXERCISE - Long Answer Type Questions8videos
HERON'S FORMULA
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR EQUATION IN TWO VARIABLESEXERCISE - Exercise 4.81videos
LINEAR EQUATION IN TWO VARIABLES
Similar Questions
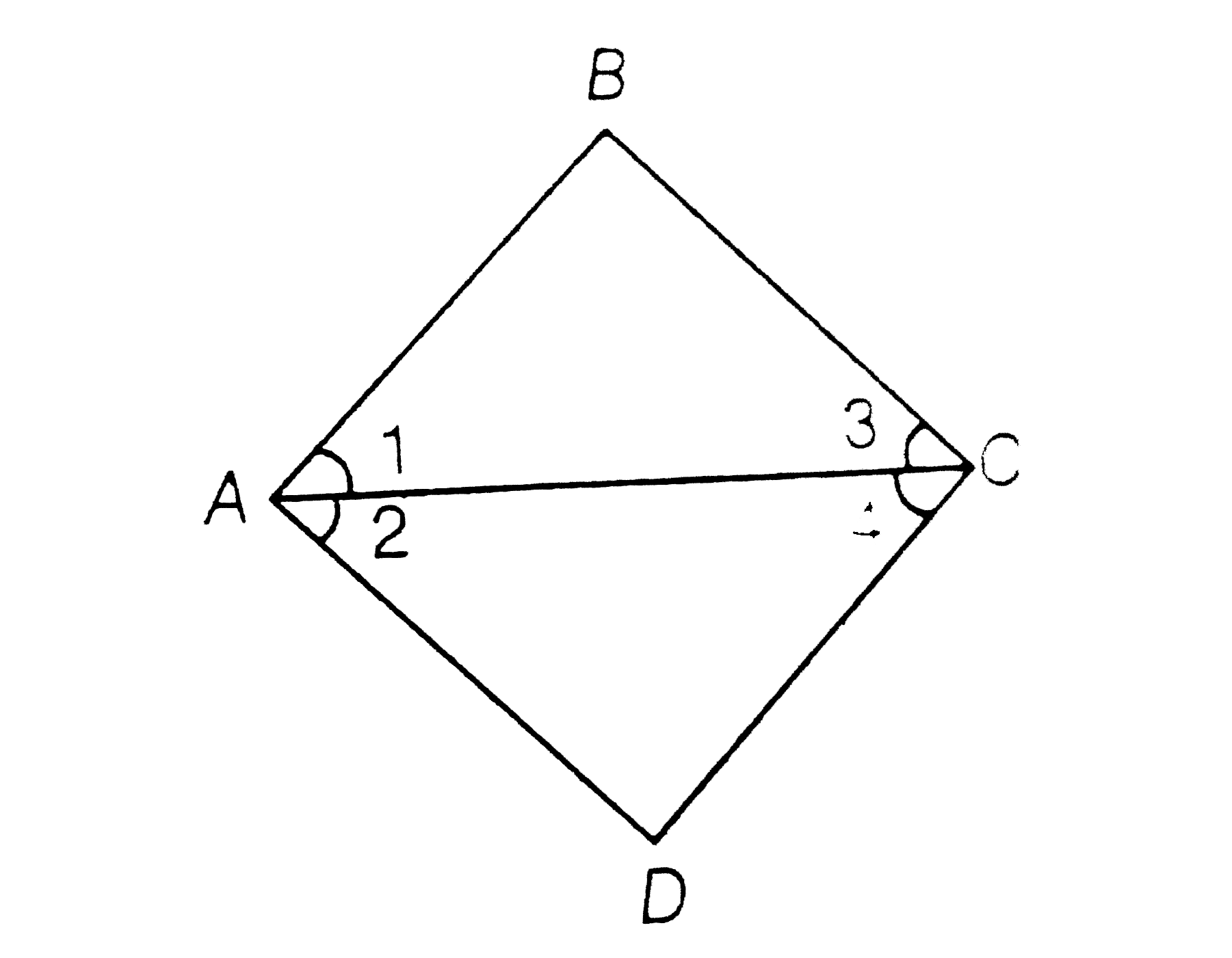
In the adjoining figure, we have ∠1=∠3and∠2=∠4. Show that ∠A=∠C.
View SolutionIn the adjoining figure, we have ∠1=∠2and=∠3. Show that ∠1=∠3.
View SolutionIn the given figure , ∠1=∠2and∠3=∠4. If BC= 7.5 cm , DE= 12.5cm and area of △ABC=13.5cm2 . Find the area of △ADE.
View SolutionIn the given figure, AC = AE, AB = AD and ∠BAD=∠EAC. Show that : BC = DE.
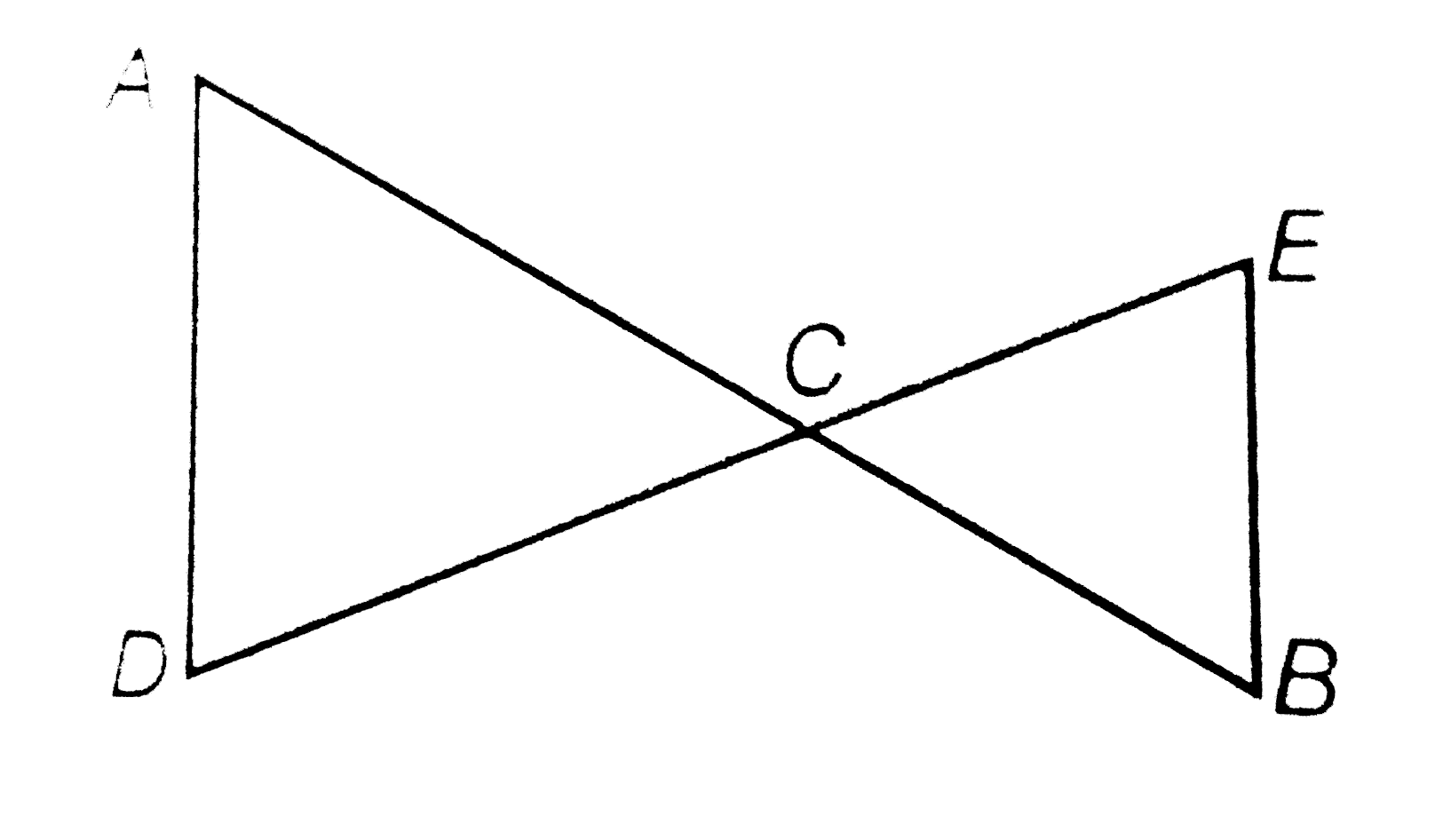
View SolutionIn the adjoining figure , we have AC=DC and CB = CE. Show that AB=DE.
View SolutionIn theadjoining figure, ∠DAB=∠ABC and AD=BC prove that BD=AC.
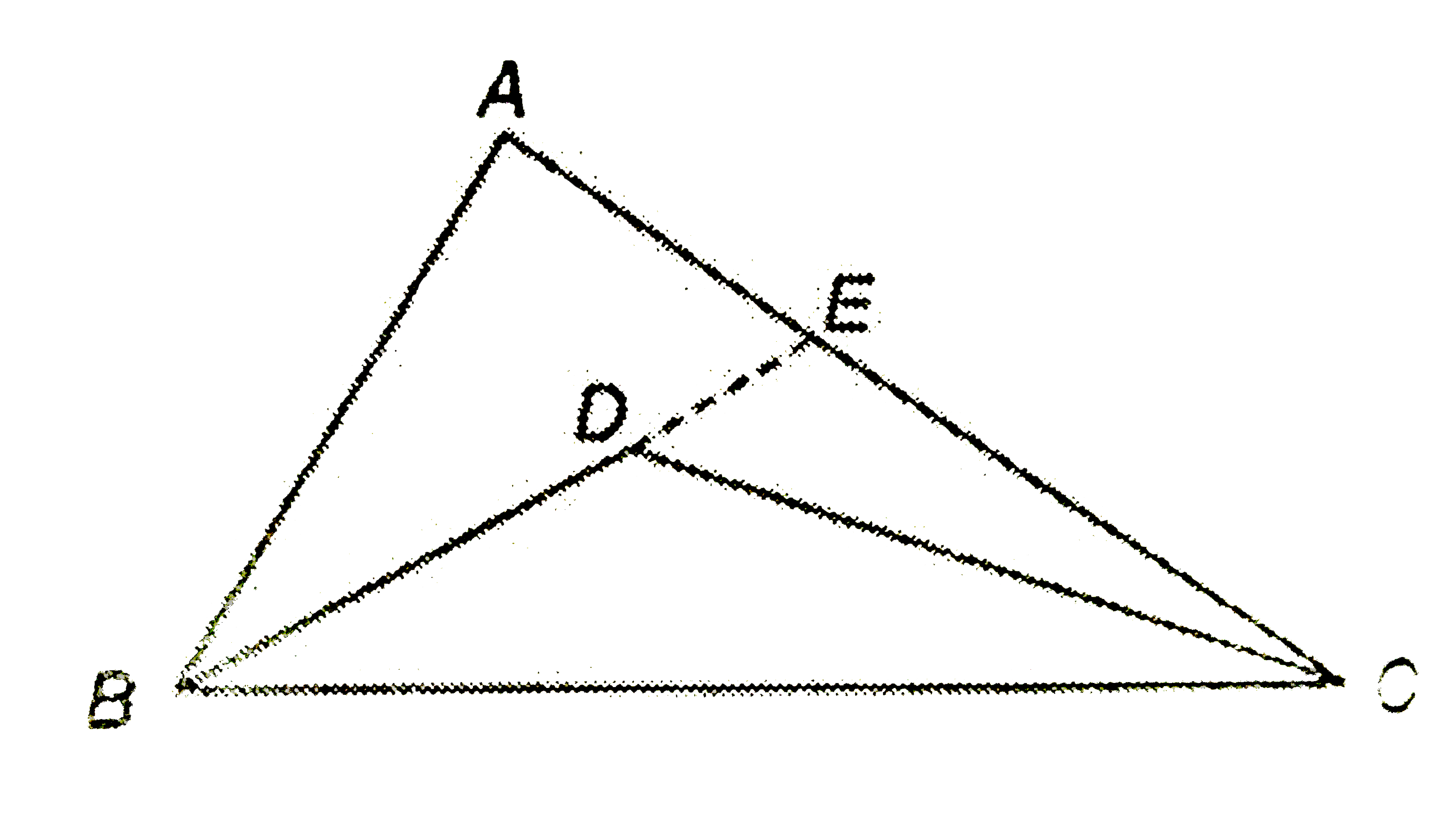
View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC<AB+AC.
View SolutionIn the given figure, find x, given that ∠1:∠2:∠3=10:5:3.
View SolutionIn the following figure, ∠BAC=60∘ and ∠ABC=65∘.
Prove that :
(i) CF>AF (ii) DC>DF
View SolutionIn the adjoining figure, ABC is a triangle right-angled at vertex A and AD is altitude.
If BD = 3.6 cm and CD = 6.4 cm, find the length of AD.View Solution