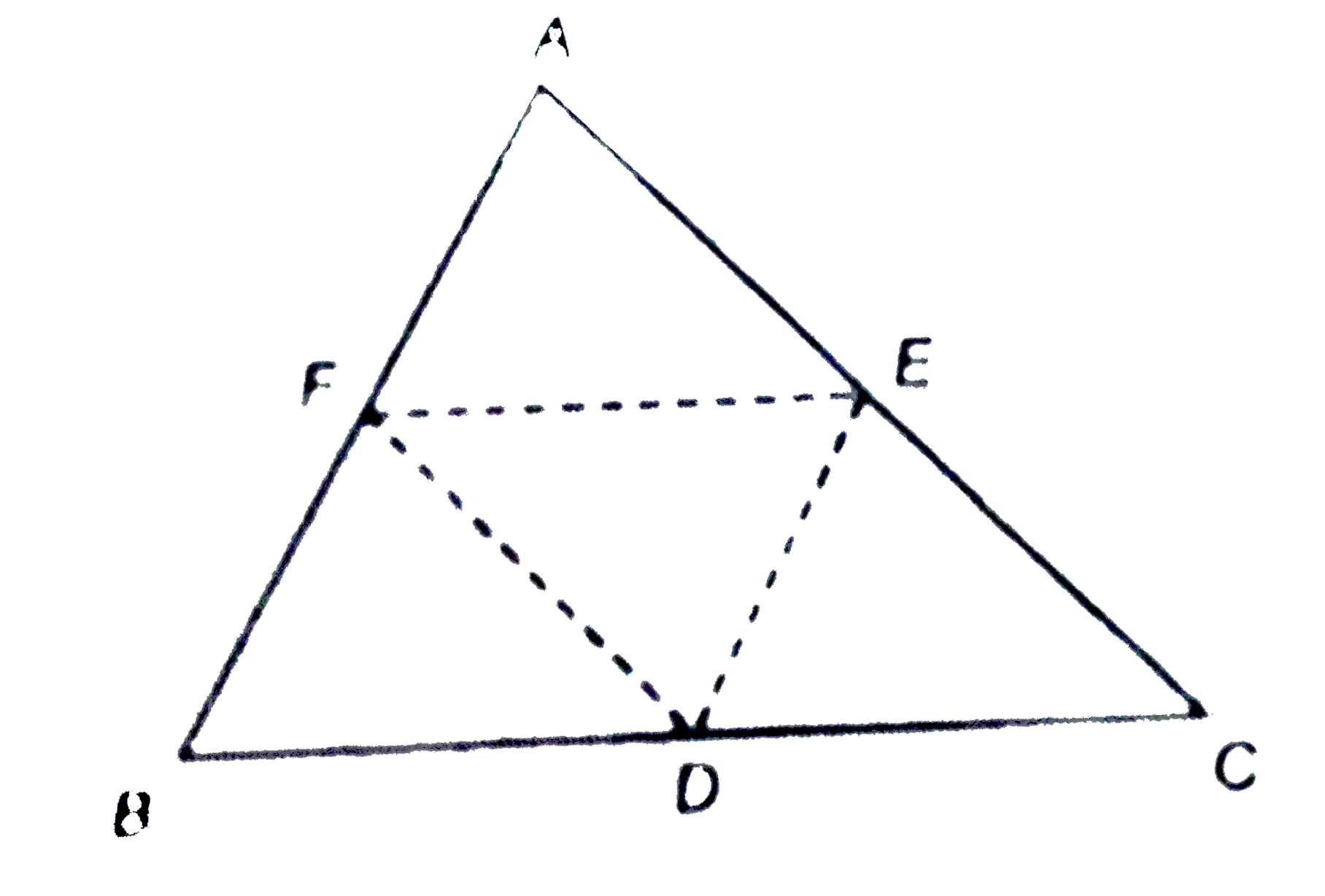
In the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

In △ABC,
F is the mid-point of AB
E is the mid point of AC
∴EF=12BC(mid point theorem)…(1)
Similarly,
FD=12AB (mid point theorem) …(2)
and ED=12AB (mid-point theorem) ...(3)
but AB =BC =CA
⇒12AB=12BC=12CA
⇒ED=EF=FD
⇒△DEF is an equilateral triangle. Hence proved.
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Problems From NCERT/exemplar
Explore 11 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- PROBABILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICSExercise:Revision Exercise
Explore 12 Videos
Similar Questions
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC. Prove that:
(i) □BDEF is a parallelogram
(ii) area of ΔDEF=14× area of ΔABC
(iii) □BDEF=12× area of ΔABC
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View SolutionD, E and F are the mid-points of the sides AB, BC and CA of an isosceles triangle ABC in which AB = BC. Prove that ΔDEF is also isosceles.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
area of BDEF is half the area of ΔABC.
View SolutionIn the adjoining figure, BM and CN are the altitudes drawn to the sides AC and AB respectively of ΔABC. If BM=CN, prove that ΔABC is isosceles.

View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC
View Solution

