Explain with the help of a labelled diagram the distribution of magnetic field due to a current through a circular loop. Why is it that if a current carrying coil has n turns, the field produced at any point is n times as large as that produced by a single turn?
To explain the distribution of the magnetic field due to a current through a circular loop, we can follow these steps:
Step 1: Understanding the Circular Loop
A circular loop carrying an electric current generates a magnetic field around it. The direction of the magnetic field can be determined using the right-hand rule: if you curl the fingers of your right hand in the direction of the current, your thumb will point in the direction of the magnetic field inside the loop.
Step 2: Drawing the Diagram
1. Draw a circle to represent the circular loop.
2. Indicate the direction of the current flowing through the loop (e.g., clockwise or counterclockwise).
3. Draw arrows to represent the magnetic field lines. Inside the loop, the magnetic field lines should be straight and parallel, indicating a uniform magnetic field. Outside the loop, the lines should curve around and eventually appear to extend straight as you move further away.
Step 3: Labeling the Diagram
- Label the circular loop as "Current-Carrying Loop."
- Mark the direction of the current with an arrow.
- Indicate the magnetic field lines with arrows, showing their direction (from North to South).
- Label the area inside the loop where the magnetic field is strong and uniform.
Step 4: Explaining the Magnetic Field Distribution
The magnetic field lines are concentrated inside the loop, where they are nearly parallel and evenly spaced, indicating a strong and uniform magnetic field. As you move away from the loop, the field lines spread out and become weaker.
Step 5: Magnetic Field Due to Multiple Turns
For a coil with n turns, the magnetic field at any point is n times larger than that produced by a single turn. This can be understood mathematically:
- The magnetic field B due to a single turn of the loop is given by the formula:
B=μ0I4πR
where μ0 is the permeability of free space, I is the current, and R is the radius of the loop.
- For n turns, the magnetic field becomes:
Bn=μ0nI4πR
- This shows that the magnetic field produced by n turns is n times that of a single turn:
Bn=n⋅B
Conclusion
Thus, the magnetic field due to a current-carrying circular loop is concentrated inside the loop, and for a coil with multiple turns, the magnetic field strength increases proportionally with the number of turns.
---
A circular loop carrying an electric current generates a magnetic field around it. The direction of the magnetic field can be determined using the right-hand rule: if you curl the fingers of your right hand in the direction of the current, your thumb will point in the direction of the magnetic field inside the loop.
1. Draw a circle to represent the circular loop.
2. Indicate the direction of the current flowing through the loop (e.g., clockwise or counterclockwise).
3. Draw arrows to represent the magnetic field lines. Inside the loop, the magnetic field lines should be straight and parallel, indicating a uniform magnetic field. Outside the loop, the lines should curve around and eventually appear to extend straight as you move further away.
- Label the circular loop as "Current-Carrying Loop."
- Mark the direction of the current with an arrow.
- Indicate the magnetic field lines with arrows, showing their direction (from North to South).
- Label the area inside the loop where the magnetic field is strong and uniform.
The magnetic field lines are concentrated inside the loop, where they are nearly parallel and evenly spaced, indicating a strong and uniform magnetic field. As you move away from the loop, the field lines spread out and become weaker.
For a coil with n turns, the magnetic field at any point is n times larger than that produced by a single turn. This can be understood mathematically:
- The magnetic field B due to a single turn of the loop is given by the formula:
B=μ0I4πR
where μ0 is the permeability of free space, I is the current, and R is the radius of the loop.
- For n turns, the magnetic field becomes:
Bn=μ0nI4πR
- This shows that the magnetic field produced by n turns is n times that of a single turn:
Bn=n⋅B
Thus, the magnetic field due to a current-carrying circular loop is concentrated inside the loop, and for a coil with multiple turns, the magnetic field strength increases proportionally with the number of turns.
Topper's Solved these Questions
- MAGNETIC EFFECTS OF ELECTRIC CURRENT BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - SHORT ANSWER TYPE QUESTIONS
12 Videos
- LIGHT : REFLECTION AND REFRACTIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LIGHT : REFLECTION AND REFRACTIONEXERCISE - Long Answer Type Questions
9 Videos
- MANAGEMENT OF NATURAL RESOURCESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MANAGEMENT OF NATURAL RESOURCESEXERCISE - Long Answer Type Questions
6 Videos
Similar Questions
The magnitude of the magnetic field at O ( centre of the circular part ) due to the current - carrying coil as shown is :
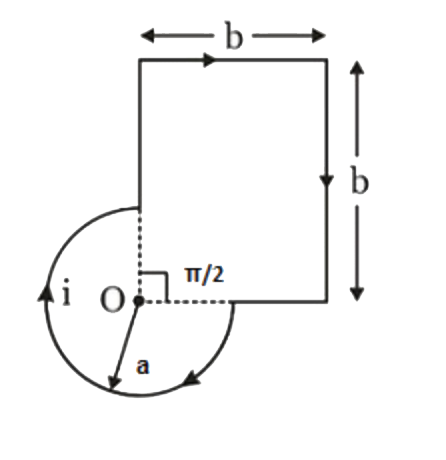
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionMagnetic field due to 0.1A current flowing through a circular coil of radius 0.1m and 1000 turns at the centre of the coil is
View SolutionDraw the pattern of magnetic field lines for a circular coil carrying current.
View SolutionThe magneitc field produced at the center of a current carrying circular coil of radius r, is
View SolutionA current - carrying loop is shown in the figure. The magnitude of the magnetic field produced at a point O is
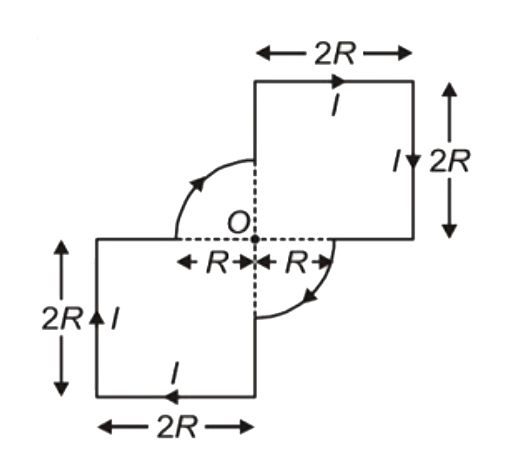
View SolutionHow will the magnetic field induction at the centre of a circular coil carrying current change, if the current through the coil is doubled and the radius of the coil is halved?
View SolutionObtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I.
View SolutionObtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I.
View SolutionThe magnetic field due to current carrying circular coil loop of radius 6 cm at a point on axis at a distance of 8 cm from the centre is 54μT . What is the value at the centre of loop ?
View Solution
