Doubtnut Promotions Sticky

A plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0
A plane EM wave travelling in vacuum along z-direction is given by E=E(0)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

(i) consider the figure given below
ocr_image
During the propagation of electromagnetic wave a along z-axis let electric field vector (E) be along x-axis and megnetic field vector B along y-axis i.e., E=E0ˆi and B=B0ˆj
Line intergral of E over the closed rectangular path 1234 in x-z plane of the figure
∮E.dl=2∫1E.dl+3∫2E.dl+4∫3E.dl+1∫4E.dl
=2∫1E.dlcos90+3∫2E.dlcos0+4∫3E.dlcos90+1∫4E.dlcos180∘
=E0h[sin(kz2−ωt)−sin(kz1−gωt)]
(ii) For evaluating ∫B.ds, let us consider the rectangle 1234 to be made of strips of are ds = hdz each.
∫B.ds=∫B.dscos0=∫B.ds=z2∫z1B0sin(kz−ωt)hdz
=−B0hk[cos(kz2−ωt)−cos(kz1−ωt)]
ocr_image
(iii) Given ∮E.dl=0dϕBdt=−ddt∮B.ds
Putting the values from Eqs. (i) and (ii) we get
E0h[sin(kz2−ωt)−sin(kz1−ωt)]
=−ddt[Byhk{cos(kz2−ωt)−cos(kz1−ωt)]
=Byhkω[sin(kz2−ωt)−sin(kz1−ωt)]
⇒ E0=B0ωK=Byc
⇒ E0B0=c
(iv) For evaluating ∮B.dl let us consider a loop 1234 in y-z plane as shown in figure given below
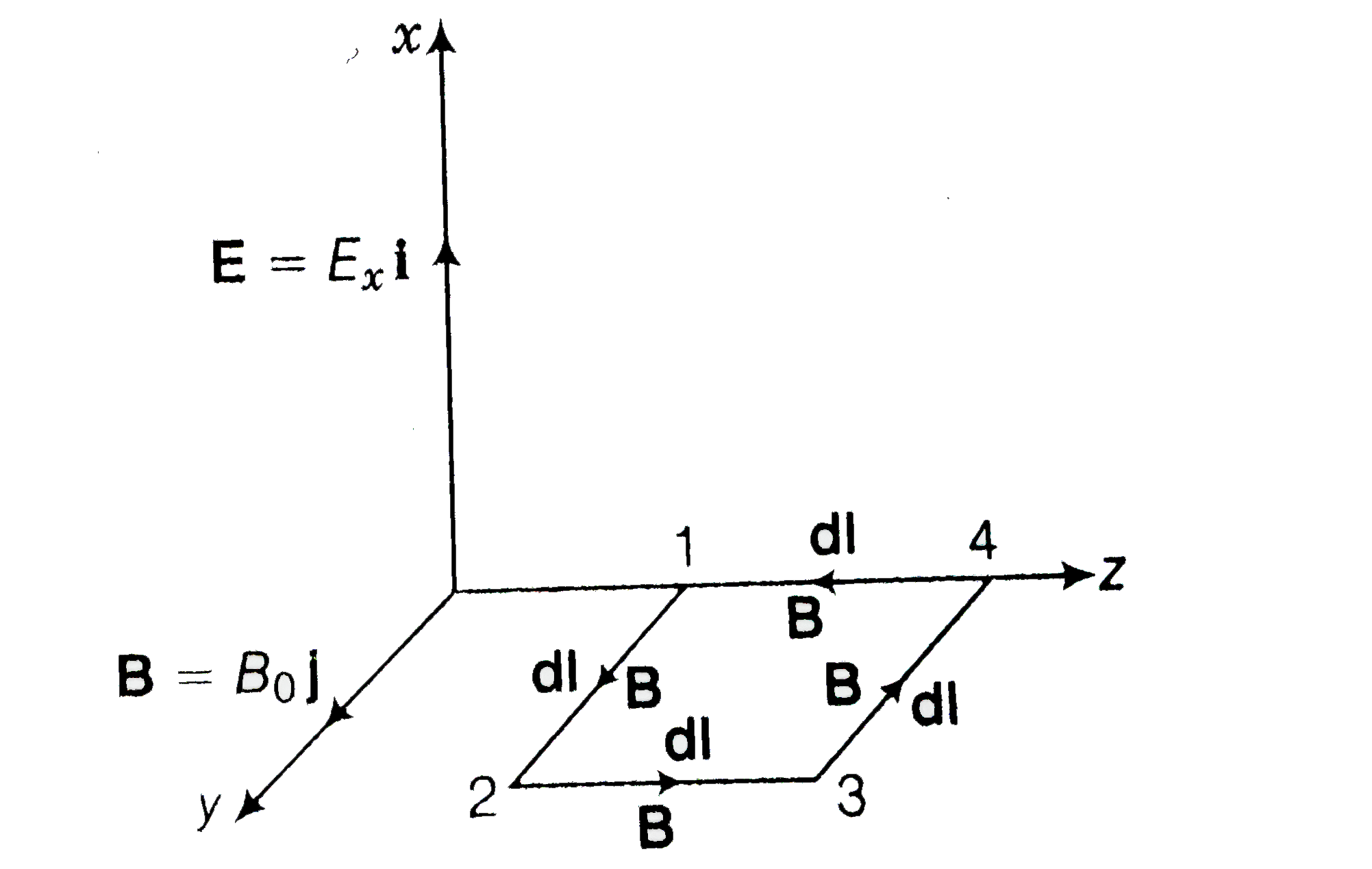
ocr_image
∮B.dl=2∫1B.dl+3∫2B.dl+4∫3B.dl+1∫4B.dl
=2∫1B.dlcos0+3∫2B.dlcos90∘+4∫3B.dlcos180∘+1∫4B.dlcos90∘
=B0h[sin(kz1−ωt)−sin(kz2−ωt)
Now to evaluate ϕE=∫E.ds let us consider the rectangle 1234 to be made of strips of area hd2 each.
ocr_image
ϕE∫E.ds=∫Edscos0=∫Eds=z2∫z1E0sin(kz1−ωt)hdz
=−E0hK[cos(kz2−ωt)−cos(kz1−ωt)]
∴dϕEdt=E0hωK[sin(kz1−ωt)−sin(kz2−ωt)]
∮B.dl=μ0(l+ε0ϕEdt)I=conduction current
∴∮B.dl=μ0εdϕEdt
Using relations obtained in Eqs. (iii) and (iv) and simplifying we get
B0=E0ωμ0ε0K
⇒ E0B0ωK=1μ0ε0
But E0B0=c and ω=ck
⇒ c.c=1μ0ε0thereforec=1√μ0ε0

|
Updated on:21/07/2023
Class 12PHYSICSELECTROMAGNETIC WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    An electromagnetic wave travelling along z-axis is given as E=E0 cos (kz−ωt). Choose the correct options from the following

    AThe associated magnetic field is given as →B=1cˆk×→E=1ω(→k×→E)
    BThe electromagnetic field can be written in terms of the associated magnetic field as →E=c(→B׈j)
    Cˆk.→E=0,ˆk.→B≠0
    Dˆk.→E=0,ˆk×→B=0
  • Question 2 - Select One

    A plane EM wave travelling along z direction is described by
    E=E0sin(kz−ωt)ˆiandB=B0sin(kz−ωt)ˆj.
    show that
    (i) The average energy density of the wave is given by uav=14ε0E20+14B20μ0.
    (ii) The time averaged intensity of the wave is given by Iav=12cε0E20.

    AThe average energy density of the wave is given by uav=14ε0E20+14B20μ0
    BThe time averaged intensity of the wave is given by Iav=12cε0E20
    CBoth (a) and (b)
    DNone of these
  • Question 3 - Select One

    If ∮sE.ds=0 Over a surface, then

    Athe electric field inside the surface and on it is zero.
    Bthe electric field inside the surface is necessarily uniform.
    Call charges must necessarily be outside the surface.
    Dall of these.