the correct order of the packing effeciency in different types of unit cells is ……….. .
fccltBcclt simple cubic
fccgt bcc gt simple cubic
fcclt bcc? Simple cubic
bcclt fccgt simple cubic
The correct Answer is:B
To determine the correct order of packing efficiency in different types of unit cells, we will calculate the packing efficiency for three types of unit cells: Simple Cubic (SC), Body-Centered Cubic (BCC), and Face-Centered Cubic (FCC).
Step 1: Calculate Packing Efficiency for Simple Cubic (SC)
1. Identify the parameters:
- Edge length of the unit cell = a
- Radius of the sphere = r
2. Relation between edge length and radius:
- For SC, spheres touch each other along the edge, so:
a=2r⇒r=a2
3. Number of spheres in the unit cell:
- There are 8 spheres at the corners, each shared by 8 unit cells:
Number of spheres=8×18=1
4. Volume of the sphere:
Vsphere=43πr3=43π(a2)3=43πa38=πa36
5. Volume of the unit cell:
Vcube=a3
6. Packing efficiency:
Packing Efficiency=VoccupiedVtotal=πa36a3=π6≈0.524or52.4%
Step 2: Calculate Packing Efficiency for Body-Centered Cubic (BCC)
1. Identify the parameters:
- Edge length of the unit cell = a
- Radius of the sphere = r
2. Number of spheres in the unit cell:
- 8 corner spheres (each contributes 18) and 1 sphere in the center:
Number of spheres=8×18+1=2
3. Volume of the sphere:
Vsphere=4πr3
4. Relation between edge length and radius:
- For BCC, the body diagonal √3a is equal to 4 times the radius:
√3a=4r⇒r=√34a
5. Volume of the unit cell:
Vcube=a3
6. Packing efficiency:
Voccupied=2×43πr3=2×43π(√34a)3=2⋅4⋅3√33⋅64πa3=3√332πa3
Packing Efficiency=3√332πa3a3≈0.6805or68.05%
Step 3: Calculate Packing Efficiency for Face-Centered Cubic (FCC)
1. Identify the parameters:
- Edge length of the unit cell = a
- Radius of the sphere = r
2. Number of spheres in the unit cell:
- 8 corner spheres and 6 face-centered spheres:
Number of spheres=8×18+6×12=4
3. Relation between edge length and radius:
- For FCC, the face diagonal √2a is equal to 4 times the radius:
√2a=4r⇒r=√24a
4. Volume of the unit cell:
Vcube=a3
5. Packing efficiency:
Voccupied=4×43πr3=4×43π(√24a)3=4⋅4⋅2√23⋅64πa3=2√23πa3
Packing Efficiency=2√23πa3a3≈0.7406or74.06%
Final Order of Packing Efficiency
Now we can summarize the packing efficiencies:
- Simple Cubic (SC): 52.4%
- Body-Centered Cubic (BCC): 68.05%
- Face-Centered Cubic (FCC): 74.06%
Thus, the correct order of packing efficiency is:
FCC>BCC>SC
- Edge length of the unit cell = a
- Radius of the sphere = r
- For SC, spheres touch each other along the edge, so:
a=2r⇒r=a2
- There are 8 spheres at the corners, each shared by 8 unit cells:
Number of spheres=8×18=1
Vsphere=43πr3=43π(a2)3=43πa38=πa36
Vcube=a3
Packing Efficiency=VoccupiedVtotal=πa36a3=π6≈0.524or52.4%
- Edge length of the unit cell = a
- Radius of the sphere = r
- 8 corner spheres (each contributes 18) and 1 sphere in the center:
Number of spheres=8×18+1=2
Vsphere=4πr3
- For BCC, the body diagonal √3a is equal to 4 times the radius:
√3a=4r⇒r=√34a
Vcube=a3
Voccupied=2×43πr3=2×43π(√34a)3=2⋅4⋅3√33⋅64πa3=3√332πa3
Packing Efficiency=3√332πa3a3≈0.6805or68.05%
- Edge length of the unit cell = a
- Radius of the sphere = r
- 8 corner spheres and 6 face-centered spheres:
Number of spheres=8×18+6×12=4
- For FCC, the face diagonal √2a is equal to 4 times the radius:
√2a=4r⇒r=√24a
Vcube=a3
Voccupied=4×43πr3=4×43π(√24a)3=4⋅4⋅2√23⋅64πa3=2√23πa3
Packing Efficiency=2√23πa3a3≈0.7406or74.06%
- Simple Cubic (SC): 52.4%
- Body-Centered Cubic (BCC): 68.05%
- Face-Centered Cubic (FCC): 74.06%
FCC>BCC>SC
Topper's Solved these Questions
- SOLID STATEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SOLID STATEEXERCISE - short answer type Questions
19 Videos
- SOLID STATEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SOLID STATEEXERCISE - matching the columns
1 Videos
- POLYMERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYMEREXERCISE - Long Answer Type Question
5 Videos
- SOLUTIONS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SOLUTIONS EXERCISE - LONG ANSWER TYPE QUESTIONS
8 Videos
Similar Questions
Knowledge Check
The correct order of the packing efficiency in different types of unit cells is
Afcc<bcc<simple cubicBfcc>bcc>simple cubicCfcc<bcc>simple cubicDbcc<fcc>simple cubic
Which of the following is correct order of packing efficiency?
View Solutionin the cubic packing , the unit cell has ………. .
View Solutionin the cubic packing , the unit cell has ………. .
View SolutionThe packing efficiency of the two-dimensional square unit cell shown below is :
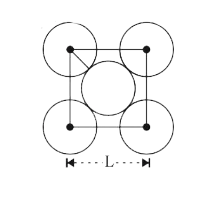
View SolutionCalculate the percentage of packing efficiency in simple cubic unit cell.
View SolutionThe correct order of the solubility of the different alcohols in water is :
View SolutionThe packing efficiency of the two dimensional square unit cell shown below is:
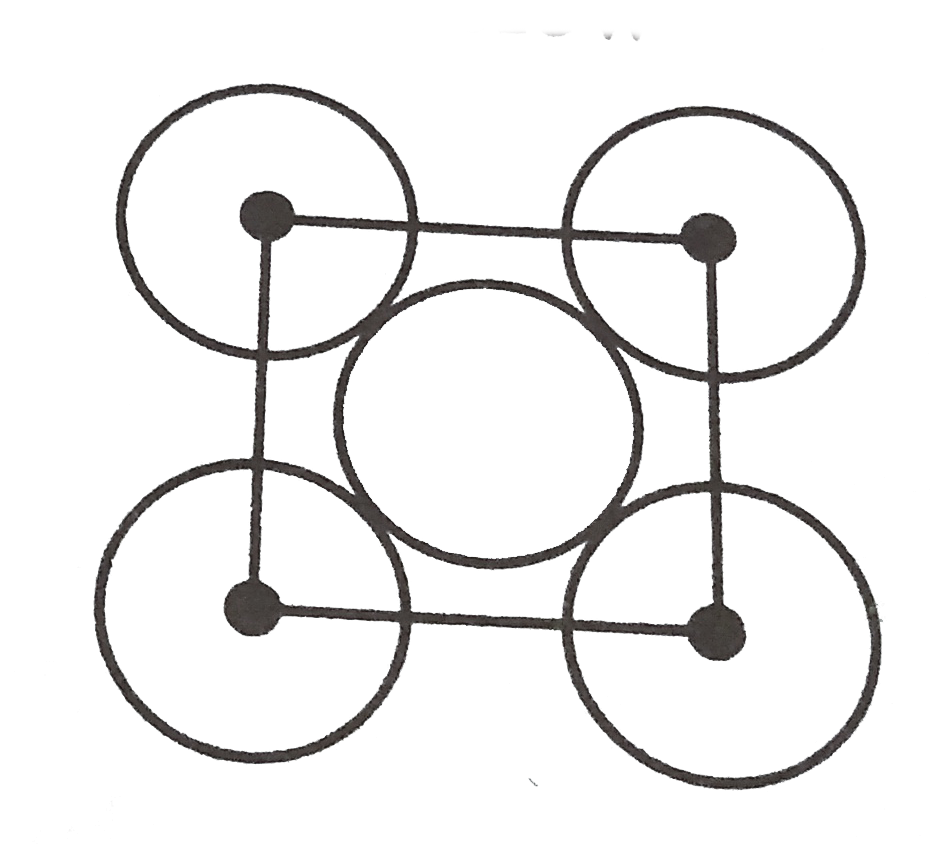
View Solution

