A rocket accelerates straight up by ejecting gas downwards. In a small time interval Δt, it ejects a gas of mass Δm at a relative speed u . Calculate KE of the entire system at t+Δt and t and show that the device that ejects gas does work =(12)Δm.u2 in this time interval (neglect gavity).
To solve the problem, we need to calculate the kinetic energy of the entire system at two different times and show that the work done by the device that ejects gas is equal to 12Δm⋅u2.
1. Define Initial Conditions:
At time t, the rocket has a mass m and a velocity v. The kinetic energy E1 at this time can be expressed as:
E1=12mv2
2. Ejecting Gas:
In a small time interval Δt, the rocket ejects a mass Δm of gas downwards with a relative speed u. After this interval, the mass of the rocket becomes m−Δm and its new velocity is v+Δv.
3. Calculate Kinetic Energy at t+Δt:
The kinetic energy E2 at time t+Δt consists of the kinetic energy of the rocket and the kinetic energy of the ejected gas:
E2=12(m−Δm)(v+Δv)2+12Δm(u−(v+Δv))2
4. Expand the Kinetic Energy Expressions:
- For the rocket:
Erocket=12(m−Δm)(v+Δv)2=12(m−Δm)(v2+2vΔv+Δv2)
- For the gas:
Egas=12Δm(u−(v+Δv))2=12Δm(u−v−Δv)2
5. Combine Kinetic Energies:
Combine the two kinetic energy expressions to find E2:
E2=12(m−Δm)(v2+2vΔv+Δv2)+12Δm(u−v−Δv)2
6. Neglect Higher Order Terms:
Since Δm and Δv are small, we can neglect the terms involving Δv2 and higher order terms. Thus, we simplify E2 to:
E2≈12mv2+12mvΔv−12Δmv2+12Δmu2−Δmuv
7. Calculate Change in Kinetic Energy:
The change in kinetic energy ΔE is given by:
ΔE=E2−E1
Substituting E1 and simplifying, we find:
ΔE=12Δmu2
8. Work-Energy Theorem:
According to the work-energy theorem, the work done W is equal to the change in kinetic energy:
W=ΔE=12Δmu2
Conclusion
Thus, we have shown that the work done by the device that ejects gas is:
W=12Δmu2
At time t, the rocket has a mass m and a velocity v. The kinetic energy E1 at this time can be expressed as:
E1=12mv2
In a small time interval Δt, the rocket ejects a mass Δm of gas downwards with a relative speed u. After this interval, the mass of the rocket becomes m−Δm and its new velocity is v+Δv.
The kinetic energy E2 at time t+Δt consists of the kinetic energy of the rocket and the kinetic energy of the ejected gas:
E2=12(m−Δm)(v+Δv)2+12Δm(u−(v+Δv))2
- For the rocket:
Erocket=12(m−Δm)(v+Δv)2=12(m−Δm)(v2+2vΔv+Δv2)
- For the gas:
Egas=12Δm(u−(v+Δv))2=12Δm(u−v−Δv)2
Combine the two kinetic energy expressions to find E2:
E2=12(m−Δm)(v2+2vΔv+Δv2)+12Δm(u−v−Δv)2
Since Δm and Δv are small, we can neglect the terms involving Δv2 and higher order terms. Thus, we simplify E2 to:
E2≈12mv2+12mvΔv−12Δmv2+12Δmu2−Δmuv
The change in kinetic energy ΔE is given by:
ΔE=E2−E1
Substituting E1 and simplifying, we find:
ΔE=12Δmu2
According to the work-energy theorem, the work done W is equal to the change in kinetic energy:
W=ΔE=12Δmu2
Thus, we have shown that the work done by the device that ejects gas is:
W=12Δmu2
Similar Questions
Suppose a rocket with an intial mass M0 eject a mass Δm in the form of gases in time Δt, then the mass of the rocket after time t is :-
View SolutionA body is thrown up in a lift with a velocity u relative to the lift, and returns to the lift in time t. Show that the lift's upward acceleration is (2u-gt)/t
View SolutionA truck moving on a smooth horizotanal surface with a uniform speed u is carrying stonedust . If a mass Δm of the stone-dust 'leaks' from the truck in a timeΔt, the force needed to keep the truck moving at its uniform speed is
View SolutionA rocket of mass 5700 kg ejects mass at a constant rate of 15 kg/s withe constant speed of 12 km/s. The acceleration of the rocket 1 minute after the blast is (g=10m/s2)
View SolutionA particle is projected with speed u at angle θ with horizontal from ground . If it is at same height from ground at time t1andt2 , then its average velocity in time interval t1 to t2 is
View SolutionA rocket is moving vertically upward against gravity. Its mass at time t is m=m0−μt and it expels burnt fuel at a speed u vertically downward relative to the rocket. Derive the equation of motion of the rocket but do not solve it. Here, μ is constant.
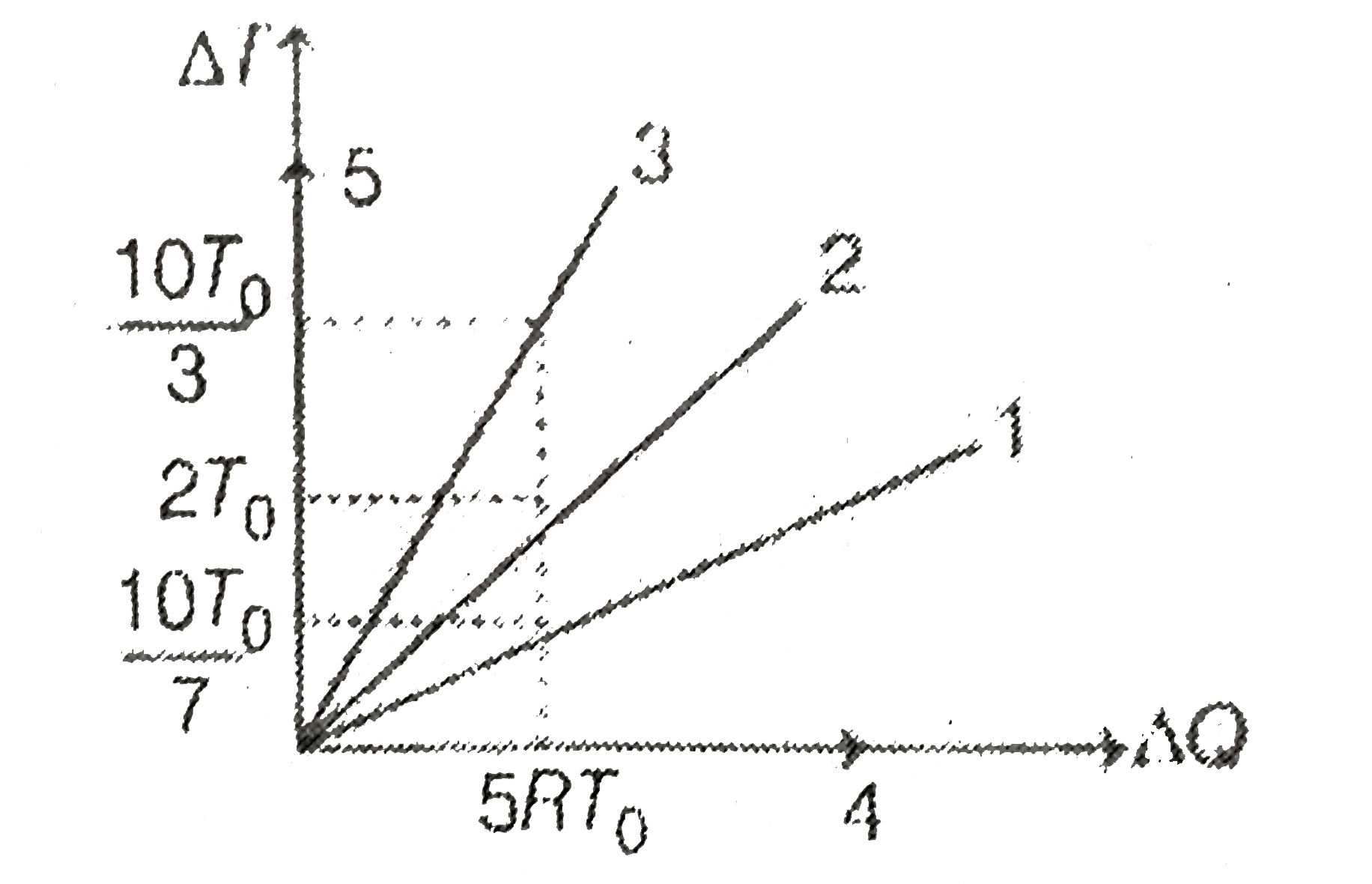
View SolutionFigure (Five straight line numbered 1, 2, 3, 4 and 5) shows graph of change in temperature ΔT verusus heat supplied ΔQ for different process performed on a gas of one mole.
View SolutionThe following graphs shows two isothermal process for a fixed mass of an ideal gas. Find the ratio of r.m.s speed of the molecules at temperatures T1 and T2?
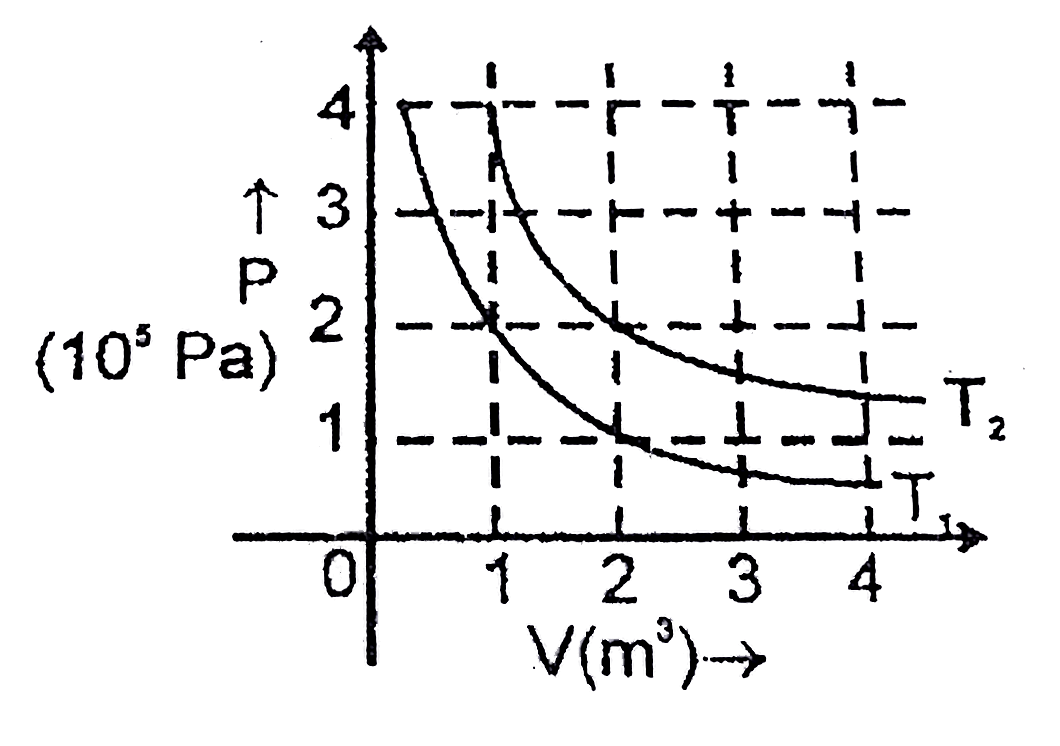
View SolutionThe following graphs shows two isotherms for a fixed mass of an ideal gas. Find the ratio of r.m.s speed of the molecules at tempertaures T1 and T2?
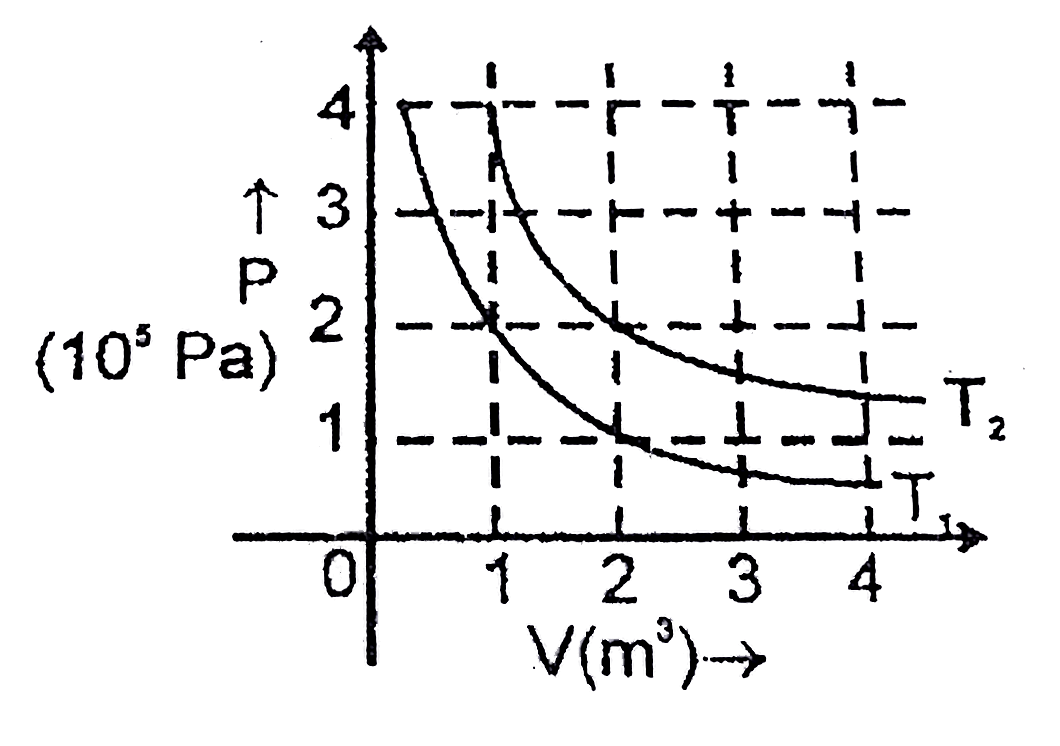
View SolutionAn elecator is going up with an upward acceleration of 1m/s2. At the instant when its velocity is 2m/s, a stone is projected upward from its floor with a speed of 2m/s relative to the elevator, at an elevation of 30∘.
(a) Calculate the time taken by the stone to return to the floor.
(b) Sketch the path of the projectile as observed by an observer outside the elevator.
(c) If the elevator was moving with a downward acceleration equal to g, how would the motion be altered?
View Solution

