A rocket is moving vertically upward against gravity. Its mass at time t is and it expels burnt fuel at a speed u vertically downward relative to the rocket. Derive the equation of motion of the rocket but do not solve it. Here, is constant.
The correct Answer is:B, D
To derive the equation of motion for the rocket, we will follow these steps:
Step 1: Define the mass of the rocket
The mass of the rocket at time t is given by:
m=m0−μt
where m0 is the initial mass of the rocket and μ is the rate at which the mass of the rocket decreases due to the expulsion of burnt fuel.
Hint: Remember that the mass decreases linearly with time due to the fuel being expelled.
Step 2: Identify forces acting on the rocket
The forces acting on the rocket are:
1. The thrust force Ft acting upwards due to the expulsion of fuel.
2. The weight W acting downwards due to gravity, which is given by W=mg.
The net force Fnet acting on the rocket can be expressed as:
Fnet=Ft−W
Hint: Consider how the thrust force is generated by the expelled fuel and how it relates to the rocket's motion.
Step 3: Express the thrust force
The thrust force can be expressed in terms of the velocity of the expelled fuel u and the rate of change of mass dmdt:
Ft=u(−dmdt)
Here, −dmdt is the rate at which mass is expelled (which is positive since mass is decreasing).
Hint: The thrust force is related to the velocity of the expelled fuel and the rate of mass loss.
Step 4: Write the equation of motion using Newton's second law
According to Newton's second law:
Fnet=mdvdt
Substituting for Fnet:
Ft−mg=mdvdt
Hint: Use the relationship between net force and acceleration to set up the equation.
Step 5: Substitute the expressions for thrust and weight
Substituting the expressions for thrust and weight into the equation gives:
u(−dmdt)−mg=mdvdt
Substituting m=m0−μt:
u(−dmdt)−(m0−μt)g=(m0−μt)dvdt
Hint: Ensure to replace the mass in the equation with its expression in terms of m0 and μt.
Step 6: Express dmdt
Since m=m0−μt, we have:
dmdt=−μ
Substituting this into the equation gives:
−u(−μ)−(m0−μt)g=(m0−μt)dvdt
Hint: This substitution simplifies the equation significantly.
Step 7: Rearrange the equation
Rearranging the equation gives:
uμ−(m0−μt)g=(m0−μt)dvdt
Hint: Isolate dvdt to express it in terms of the other variables.
Final Equation
The final form of the equation of motion is:
(m0−μt)dvdt=uμ−(m0−μt)g
This is the required equation of motion for the rocket.
The mass of the rocket at time t is given by:
m=m0−μt
where m0 is the initial mass of the rocket and μ is the rate at which the mass of the rocket decreases due to the expulsion of burnt fuel.
The forces acting on the rocket are:
1. The thrust force Ft acting upwards due to the expulsion of fuel.
2. The weight W acting downwards due to gravity, which is given by W=mg.
Fnet=Ft−W
The thrust force can be expressed in terms of the velocity of the expelled fuel u and the rate of change of mass dmdt:
Ft=u(−dmdt)
Here, −dmdt is the rate at which mass is expelled (which is positive since mass is decreasing).
According to Newton's second law:
Fnet=mdvdt
Substituting for Fnet:
Ft−mg=mdvdt
Substituting the expressions for thrust and weight into the equation gives:
u(−dmdt)−mg=mdvdt
Substituting m=m0−μt:
u(−dmdt)−(m0−μt)g=(m0−μt)dvdt
Since m=m0−μt, we have:
dmdt=−μ
Substituting this into the equation gives:
−u(−μ)−(m0−μt)g=(m0−μt)dvdt
Rearranging the equation gives:
uμ−(m0−μt)g=(m0−μt)dvdt
The final form of the equation of motion is:
(m0−μt)dvdt=uμ−(m0−μt)g
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Exercise 11.5
Explore 4 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Exercise 11.6
Explore 11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Exercise 11.3
Explore 7 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
A rocket with an initial mass of 1000kg, is launched vertically upward from rest under gravity. The rocket burns fuel at the rate of 10kg per second. The burnt matter is ejected vertically downwards with a speed of 2000m/s relative to the rocket . Find the velocity of the rocket after 1min of start.
View SolutionA rocket of initial mass m0 has a mass m0(1−t/3) at time t. The rocket is lauched from rest vertically upwards under gravity and expels burnt fuel at a speed u relative to the rocket vertically downward. Find the speed of rocket at t=1.
View SolutionA rocket, with an initial mass of 1000kg, is launched vertically upwards from rest under gravity. The rocket burns fuel at the rate of 10kg per second. The burnt matter is ejected vertically downwards with a speed of 2000ms−1 relative to the rocket. If burning ceases after one minute, find the maximum velocity of the rocket. (Take g as constant at 10ms−2)
View SolutionA rocket of mass 1000 kg is to be projected vertically upwards. The gases are exhausted vertically downwards with velocity 100m/s with respect to the rocket. (What is the minimum rate of burning fuel, so as to just lift the rocket upwards against the gravitational attraction?) (Take g=10m/s2)
View Solution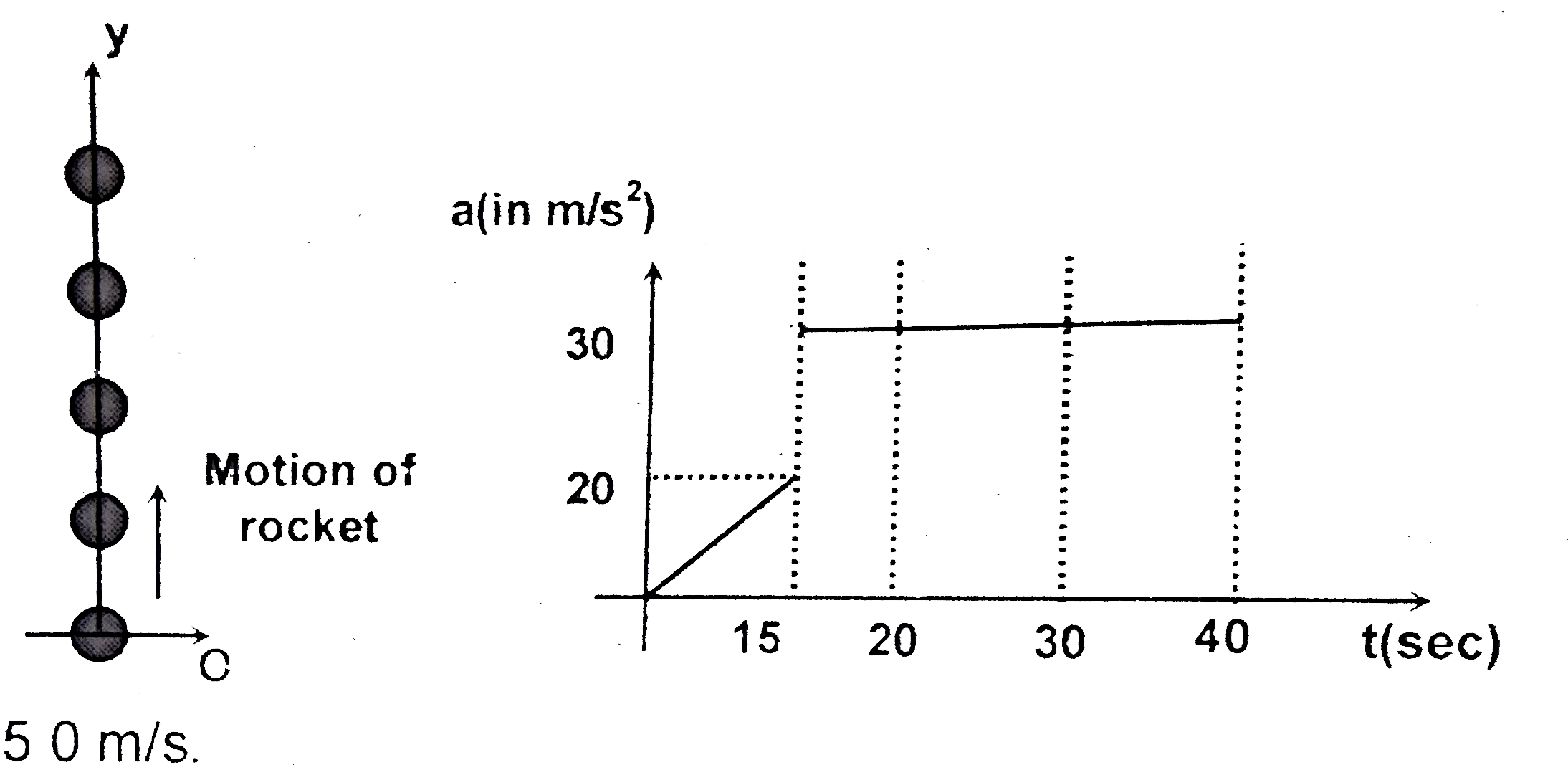
A two stage rocket is fired vertically upward from rest with acceleration as shown in a-t graphs. After 15 sec, the first stage burns out and second stage ignites. Choose the INCORRECT statement regarding motion of rocket in the time interval 0≤t≤40s.
View Solution
A container filled with viscous liquid is moving vertically downwards with constant speed 3v0. At the instant shown, a sphere of radius r is moving vertically downwards (in liquid) has speed v0. The coefficient of viscosity is η. There is no relative motion between the liquid and the container. Then at the shoen instant, The magnitude of viscous force acting on sphere is
View SolutionA body is projected vertically upward with speed 10m/s and other at same time with same speed in downward direction from the top of a tower. The magnitude of acceleration of first body w.r.t. second is {take g=10m/s2}
View SolutionA rocket of initial mass 6000kg ejects mass at constant rate of 200 kg/sec. with constant relative speed of 800 m/sec. The acceleration of the rocket after 5 sec is (neglect gravity)
View SolutionA model rocket rests on a frictionless horizontal surface and is joined by a string of length l to a fixed point so that the rocket moves in a horizontal circular path of radius l. The string will break if its tensiion exceeds a value T. The rocket engine provides a thrust F of constant magnitude along the rocket's direction of motion. the rocket has a mass m that does not change with time. Answer the following questions based on the above passage.
What distance does the rocket travel between the time t1 when the string breaks and the time 2t1? The rocket engine continues of operate after the string breaks.
View SolutionA model rocket rests on a frictionless horizontal surface and is joined by a string of length l to a fixed point so that the rocket moves in a horizontal circular path of radius l. The string will break if its tensiion exceeds a value T. The rocket engine provides a thrust F of constant magnitude along the rocket's direction of motion. the rocket has a mass m that does not change with time. Answer the following questions based on the above passage.
Starting from rest at t=0 at what later time t1 is the rocket travelling so fast that the string breaks. Ignnore any air resistance.
View Solution