Derive an expression for the torque acting or a current carrying loop which subtends angle with uniform magnetic field.Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

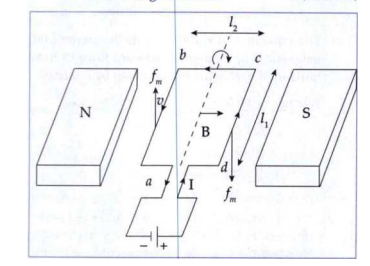
1. As shown in figure plane ABCD is not along the magnetic field but makes an angle with it.

2. We take the angle between the field and the normal to the coil to be angle $θ$ .
3. The forces on the arms BC and DA are equal, opposite and act along the axis of the coil, which connects the centres of mass of BC and DA. Being collinear along the axis they cancel each other, resulting in no net force or torque.
4. The forces on arms AB and CD are ${\to F}_{1} and {\to F}_{2}$ respectively.
They too are equal and opposite with magnitude $F_{1} = F_{2} = I b B$ .

5. In figure is a view of the arrangement from the AD and it illustrates these two forces constituting a couple. The magnitude of the torque on the loop is,
$τ = τ_{1} + τ_{2}$
$τ = F_{1} (\frac{a}{2} sin θ) + F_{2} (\frac{a}{2} sin θ)$
$[∵ τ = (magnitude of force) \times (perpendicular distance from reference points)]$
$τ = (I b B) (\frac{a}{2} sin θ) + (I b B) (\frac{a}{2} sin θ)$
$τ = I (a b) B sin θ$
$τ = I A B sin θ ... (1)$
$\to τ = I \to A \times \to B ... (2)$
6. As $θ \to 0$ , the perpendicular distance between the forces of the couple also approaches zero. This makes the forces collinear and the net force and torque zero.
7. But, magnetic moment of the current loop as,
$\to m = I \to A ... (3)$
8. Where the direction of the area vector $\to A$ is given by the right hand thumb rule and is directed into the plane of the paper.
9. Angle between $\to m and \to B is θ$ , so from equation (2), (3) we can write,
$\to τ = \to m \times \to B ... (4)$
10. For N number of turns in coil,
$\to τ = N I \to A \times \to B$
= NIAB, where $\to m = N I \to A$
(This equation is analogous to the electrostatic case, $\to τ = {\to p}_{e} \times \to E$ )

Updated on:21/07/2023

|

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-MOVING CHARGES AND MAGNETISM-SECTION D (MCQs ASKED IN COMPETITIVE EXAMS)

Home
Ask Doubt
Profile