Derive an expression for the torque acting on a current carrying loop suspended in a uniform magnetic field.Solution in Gujrati
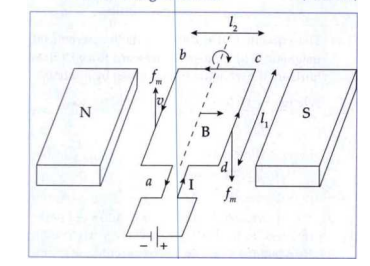
1. As shown in figure, consider a rectangular coil ABCD suspended in a uniform magnetic field , with its axis perpendicular to the field.


2. Suppose, current flowing through coil ABCD be I, AB = DC = b and AD = BC = a and area be A = ab.
2. The field exerts no force on the two arms AD and BC of the loop, because both are parallel to each other,
3. Sides AB and CD of coils are perpendicular to magnetic field.
4. So, force on side AB is,
5. Similarly it exerts a force on the arm CD and is directed out of the plane of the paper,
6. Thus, the net force on the loop is zero. There is a torque on the loop due to the pair of forces .
7. Figure (b) shows a view of the loop from the AD end. It shows that the torque on the loop tends to rotate it anti-clockwise.
8. Resultant torque on coil is given by,
=
=
where A = ab that is area of rectangle.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:KUMAR PRAKASHANChapter:MOVING CHARGES AND MAGNETISMExercise:SECTION A (TRY YOURSELF)
Explore 89 Videos
- MOVING CHARGES AND MAGNETISMBook:KUMAR PRAKASHANChapter:MOVING CHARGES AND MAGNETISMExercise:SECTION B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
Explore 22 Videos
- MAGNETISM AND MATTERBook:KUMAR PRAKASHANChapter:MAGNETISM AND MATTERExercise:SECTION D Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams) MCQs asked in Board Exam and GUJCET
Explore 7 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:KUMAR PRAKASHANChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:SECTION-D (MULTIPLE CHOICE QUESTIONS (MCQs))(MCQs ASKED IN COMPETITIVE EXAMS)
Explore 142 Videos
Similar Questions
State Oersted's experiment.
View SolutionA straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid air by a uniform horizontal magnetic field B (figure). What is the magnitude of the magnetic field ?

View SolutionAt a place on earth the vertical component of earth's magnetic field is √3 times its horizontal component. The angle of dip at this place is …...
View SolutionWhich of the following is used in optical fibres ?
View SolutionIn radial magnetic field , the torque acting on the current carrying freely suspended coil is
View SolutionWhat is the torque on a current carrying loop placed in a uniform magnetic field?
View SolutionCurrent Carrying Loop in Uniform Magnetic Field|Torque on a Loop
View SolutionDerive an expression for the torque acting or a current carrying loop which subtends angle with uniform magnetic field.
View SolutionDerive an expression for the torque acting on a rectangular current carrying loop suspended in a uniform magnetic field.
View SolutionFind an expression for the torque acting on a current carrying loop suspended in a uniform magnetic field. Under what conditions this torque will be maximum and minimum ?
View SolutionDerive an expression for torque acting on a bar magnet placed in a uniform magnetic field.
View SolutionDerive an expression for Torque acting on a bar magnet placed in a uniform magnetic field.
View SolutionDerive an expression for torque acting on a rectangular current loop carrying coil placed in a uniform magnetic field.
View SolutionA rectangular loop of area A and carrying a steady current I is placed in a uniform magnetic field:-Derive the expression of torque, tau = barmxxbarB acting on the loop.
View SolutionA rectangular loop carrying a steady current is placed in a uniform magnetic field. Obtain the expression for the torque acting on the loop.
View Solution