A rectangular pipe having cross-sectional area A is closed at one end and at its other end a block having same cross-section is placed so that the system is airtight. In the equilibrium position of the block, the pressure and volume of air enclosed in the pipe and P and V respectively. Prove that the block performs SHM when it is given a small displacement 'x' inward and released. Also find the period of this SHM. Assume the walls to be frictionless and compression of air to be isothermal.Solution in Gujrati
Due to small compression, suppose increase in pressure =△P and decrease in volume =△V
For isothermal compression, (P+△P)(V−△P)=PV (From Boyle.s law, PV= constant)

∴PV−P△V+V△P−△P△V=PV
Now, △PV is very small compared to the other terms hence neglacting △P△V and taking △P as subject to formula.
△P=P△VV=PAxV(∴△V=Ax) .........(1)
Restoring force acting on the block in the direction opposite to the displacement due to this excess pressure.
F=A△P .........(2)
Putting value of △P from equation (1) in equation (2),
F=(PA2V)x=kx,
where k=PA2V= constant.
This force is opposite to the displacement and is directly porportional to it hence block performs SHM.
Now, Periodic time T=2π√mk
∴T=2π√mPA2/V [∴ Putting value of k ]
∴T=2π(mVPA2)12.
Topper's Solved these Questions
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-C (OBJECTIVE QUESTIONS)
60 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-C (OBJECTIVE QUESTIONS TRUE OR FALSE)
8 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (ADDITIONAL EXERCISE)
9 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)
5 Videos
- PHYSICAL WORLDBOOK - KUMAR PRAKASHANCHAPTER - PHYSICAL WORLDEXERCISE - SECTION-E (QUESTIONS FROM MODULE)
9 Videos
Similar Questions
What is the phase difference between the velocity and displacement of a paticle executing SHM?
View SolutionThe acceleration of SHO at mean position is maximum.
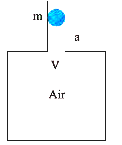
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View SolutionA block having equilateral triangular cross-section of side a and mass m is placed on a rough inclined surface, so that it remains in equilibrium as shown in figure. The torque of normal force acting on the block about its centre of mass is
View Solution_S01_005_Q01.png)
Find out the elongation in block. If mass area of cross-section and young modulus of block are m, A and y respectively.
View SolutionA wire of length l, area of cross-section A and Young,s modulus of elasticity Y is suspended form the roof of a building. A block of mass m is attached at lower end of the wire. If the block is displaced from its mean position and released then the block starts oscillating. Time period of these oscillations will be

View SolutionA block of rectangular size of mass m and area of cross section A, float in a liquid of density ρ.If we give a small vertical displacement from equilibrium, It undergoes SHM with time period T, then
View SolutionA rectangular pipe having cross sectional area A. It is closed at one end and at its other end ablock having same cross-section and mass 'm' is placed such that system is air tight. Inequilibrium position of block the pressure and volume of air enclosed in pipe are P and Vrespectively. If block is displaced by small distance x inward and released then find the timeperiod of S.H.M. [Assume the walls are frictionless and compression of air is isothermal].
View SolutionA wooden block of cross-sectional area 10cm2 is floating vertically on water. The volume of the immersed portion of the block is 200cm3. The block is depressed slightly inside water and then released. Calculate the time period of vibration of the block.
View SolutionA wooden block of cross sectional area 10cm2 remains floating upright in water. The volume of the immersed part of the block is 200cm3. If the block is depressed slightly and then released, determine the time period of its oscillation.
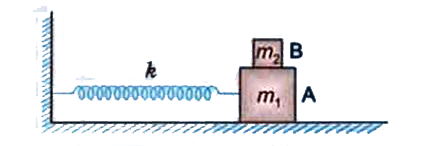
View SolutionA block A of mass m1 is placed on a horizontal frictionless table. It is connected to one end of a light spring of force constant k whose other end is fixed to a wall. A small block B of mass m2 is placed on block A. The coefficient of static friction between the blocks is μ. The system is displaced slightly from its equilibrium position and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block ?
View SolutionA rectangular block of mass m and area of cross section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium it undergoes with a time period T, then
View SolutionA horizontal pipe of area of cross-section a and 3a respectively, then the ratio of velocity of flow at two different cross-section (If flow is streamline) is
View Solution
