Two simple harmonic motions are represented by y1=10sinπ4(12t+1) and y2=5(sin3πt+√3cos3πt). Find out the ratio of their amplitudes. What are the time period of two motions.Solution in Gujrati
y1=10sin(π)4(12t+1)
Comparing y1=10sin(3πt+π4) with y=A1sin(ω1t+ϕ)
Amplitude A1=10cm and ω=3πrads−1
T=2πω=2π3π=23s
and y2=5(sin3πt+√3cos3πt)
=5×2[12sin3πt+√32(cos3πt)]
y2=2×5[cosϕsin3πt+sinϕ(cos3πt)]
Comparing Y2=10[sin(3π+ϕ)] with y=A2sin(ω2t+ϕ)
Amplitude A2=10cm and ω23πrads−1
∴T2=2πω2=2π3π=23 second
Ratio of amplitudes A1A2=1010=1
and T1=T2=23 second .
Topper's Solved these Questions
- OSCILLATIONSBook:KUMAR PRAKASHANChapter:OSCILLATIONSExercise:SECTION-C (OBJECTIVE QUESTIONS)
Explore 60 Videos
- OSCILLATIONSBook:KUMAR PRAKASHANChapter:OSCILLATIONSExercise:SECTION-C (OBJECTIVE QUESTIONS TRUE OR FALSE)
Explore 8 Videos
- OSCILLATIONSBook:KUMAR PRAKASHANChapter:OSCILLATIONSExercise:SECTION-B (ADDITIONAL EXERCISE)
Explore 9 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE Book:KUMAR PRAKASHANChapter:OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE Exercise:CHAPTER - 8 (Match Type questions)
Explore 5 Videos
- PHYSICAL WORLDBook:KUMAR PRAKASHANChapter:PHYSICAL WORLDExercise:SECTION-E (QUESTIONS FROM MODULE)
Explore 9 Videos
Similar Questions
What is the phase difference between the velocity and displacement of a paticle executing SHM?
View SolutionThe acceleration of SHO at mean position is maximum.
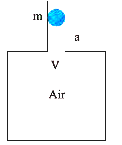
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View SolutionTwo simple harmonic motions are represented by the equations
y1=10sin(3πt+π/4)andy2=5(sin3πt+√3cos3πt) their amplitude are in the ratio of ………… .
View SolutionTwo simple harmonic motion are represent by the following equations y_(1) = 10 sin (pi//4) (12 t + 1) y_(2) = 5 (sin 3 theta t + sqrt3 cos 3 theta t) Here t is in seconds. Find out the ratio of their amplitudes.What are the time period of the two motion?
View SolutionTwo simple harmonic motions are represented by the equations y1=10sin(3πt+π4)
and y2=5(3sin3πt+√3cos3πt). Their amplitudes are in the ratio of
View SolutionTwo simple harmonic motions are represented by the equations.
y1=10sinπ4(12t+1),y2=5(sin3pt+√3cos3pt) the ratio of their amplitudes is
View SolutionTwo simple harmonic motions are represented by y_(1)=5 [sin 2 pi t + sqrt(3)cos 2 pi t] and y_(2) = 5 sin (2pit+(pi)/(4)) The ratio of their amplitudes is
View SolutionTwo simple harmonic motions are represented as y1=10sinω and y2=5sinwt+5cosωt
The ration of the amplitudes of y1 and y2 is
View SolutionA simple harmonic motion is represented by : y=5(sin3πt+√3cos3πt)cm The amplitude and time period of the motion are :
View Solutionदो सरल आवर्त गतियाँ y1=10sin(3πt+π4) तथा y2=5[sin3πt+√3cos3πt] समीकरणों से प्रदर्शित की जाती है। इनके आयामों का अनुपात............. है, इन गतियों के आवर्तकाल.............. हैं।
View SolutionTwo simple harmonic motions are represented by the equations
y1=8sin(π)4(10t+2),y2=6(sin5πt+√3cos5ωt)
IF the ratio of amplitudes of y1andy2 is α and their respective ratio of time periods is β, then find β/α.
View SolutionIf two SHMs are represented by equations y_(1) = 5 sin (2pi t + pi//6) and y_(2) = 5 [sin (3pi) + sqrt3 cos (3pi t)] . Find the ratio of their amplitudes.
View Solution

