A wooden block of cross sectional area 10cm2 remains floating upright in water. The volume of the immersed part of the block is 200cm3. If the block is depressed slightly and then released, determine the time period of its oscillation.
The correct Answer is:0.9 s (approx.)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:CHHAYA PUBLICATIONChapter:SIMPLE HARMONIC MOTIONExercise:ASSERTION-REASON TYPE
Explore 3 Videos
- SIMPLE HARMONIC MOTIONBook:CHHAYA PUBLICATIONChapter:SIMPLE HARMONIC MOTIONExercise:MULTIPLE CORRECT ANSWER TYPE
Explore 6 Videos
- SIMPLE HARMONIC MOTIONBook:CHHAYA PUBLICATIONChapter:SIMPLE HARMONIC MOTIONExercise:PROBLEM SET - II
Explore 32 Videos
- ROTATION OF RIGID BODIES Book:CHHAYA PUBLICATIONChapter:ROTATION OF RIGID BODIES Exercise:CBSE SCANNER
Explore 10 Videos
- STATICSBook:CHHAYA PUBLICATIONChapter:STATICSExercise:CBSE SCANNER
Explore 3 Videos
Similar Questions
A cylindrical of wood (density =600kgm−3) of base area 30cm2 and height 54cm, floats in a liquid of density 900kg−3 The block is deapressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly) :
View Solution(i) A cylindrical container has area of cross section equal to 4A and it contains a non viscous liquid of density 2ρ. A wooden cylinder of cross sectional area A and length L has density ρ. It is held vertically with its lower surface touching the liquid. It is released from this position. Assume that the depth of the container is sufficient and the cylinder does not touch the bottom.
(a) Find amplitude of oscillation of the wooden cylinder.
(b) Find time period of its oscillation.
Two cubical blocks of side length a and 2a are stuck symmetrically as shown in the figure. The combined block is floating in water with the bigger block just submerged completely. The block is pushed down a little and released. Find the time period of its oscillation. Neglect viscostiy.

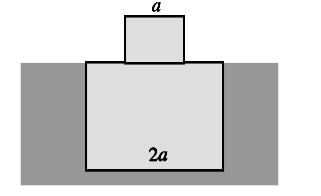
View Solution
Knowledge Check
A cylindrical of wood (density =600kgm−3) of base area 30cm2 and height 54cm, floats in a liquid of density 900kg−3 The block is deapressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly) :
A26cmB52cmC36cmD65cmA wire of length l, area of cross-section A and Young,s modulus of elasticity Y is suspended form the roof of a building. A block of mass m is attached at lower end of the wire. If the block is displaced from its mean position and released then the block starts oscillating. Time period of these oscillations will be
 A2π√AlmYB2π√AYmlC2π√mlYAD2π√mYal
A2π√AlmYB2π√AYmlC2π√mlYAD2π√mYalA pole is floating in a liquid with 80 cm of its length immersed. It is pushed doun a certain distance and then released. Time period of vertical oscillation is
A4π7sB3π7sC2π7sDπ7s
A wooden block of mass 20 gram and cross section 20 cm2 is floating on the surface of water. If it is slightly depressed and released from the equilibrium position, then calculate the frequency of oscillation of the block if specific gravity of wood is 0.28.
View SolutionA block of wood of volume 30cm3 floats in water with 20cm3 of its volume immersed.
Calculate the weight of the block of wood .
View SolutionA block of wood of volume 30cm3 floats it water with 20cm3 of its volume immersed.
Calculate the density.
View SolutionA wooden block of cross sectional area A (in shape of a rectangle) has height h. It is held such that its lower surface touches the water surface in a wide and deep tank. The block is released in this positon. It oscillates for some time and then settles into its equilibrium positon. in equilibrium the block floats with its upper face just on the water surface. Calculate the amount of heat generated in the process assuming that the loss in gravitational potential energy of the system coprising of water and the block gets converted into heat. Density of water is ρ.
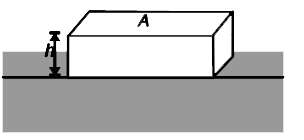
View SolutionA wire of length l, area of cross-section A and Young,s modulus of elasticity Y is suspended form the roof of a building. A block of mass m is attached at lower end of the wire. If the block is displaced from its mean position and released then the block starts oscillating. Time period of these oscillations will be

View Solution

