Kavita obtained 16, 14, 18 and 20 marks (out of 25) in Maths in weekly tests in the month of Jan. 2000, then mean marks of Kavita is
18
16.5
17
17.5
The correct Answer is:C
To find the mean marks of Kavita, we will follow these steps:
Step 1: Write down the marks obtained by Kavita.
Kavita obtained the following marks in her weekly tests:
- Test 1: 16
- Test 2: 14
- Test 3: 18
- Test 4: 20
Step 2: Calculate the sum of the marks.
Now, we will add these marks together:
Sum=16+14+18+20
Calculating this gives:
Sum=68
Step 3: Count the number of observations.
Next, we need to determine how many tests (observations) there are. Kavita has taken 4 tests:
- Total number of observations = 4
Step 4: Apply the formula for mean.
The formula for calculating the mean is:
Mean=Sum of all observationsTotal number of observations
Substituting the values we found:
Mean=684
Step 5: Calculate the mean.
Now, we perform the division:
Mean=17
Conclusion:
Thus, the mean marks of Kavita is 17.
---
Kavita obtained the following marks in her weekly tests:
- Test 1: 16
- Test 2: 14
- Test 3: 18
- Test 4: 20
Now, we will add these marks together:
Sum=16+14+18+20
Calculating this gives:
Sum=68
Next, we need to determine how many tests (observations) there are. Kavita has taken 4 tests:
- Total number of observations = 4
The formula for calculating the mean is:
Mean=Sum of all observationsTotal number of observations
Substituting the values we found:
Mean=684
Now, we perform the division:
Mean=17
Thus, the mean marks of Kavita is 17.
Topper's Solved these Questions
Similar Questions
The marks (out of 100) obtained by you in 6 class test are 99,100,95,60,70,90 find median .
View Solution60 students of Section A of Class XI, obtained 40 mean marks in Statistics, 40 students of Section B obtained 35 mean marks in Statistics. Find out mean marks in Statistics for Class XI as a whole.
View Solution
Knowledge Check
The table shows the marks obtained by 25 students in a class test. Find the mean of the marks obtained
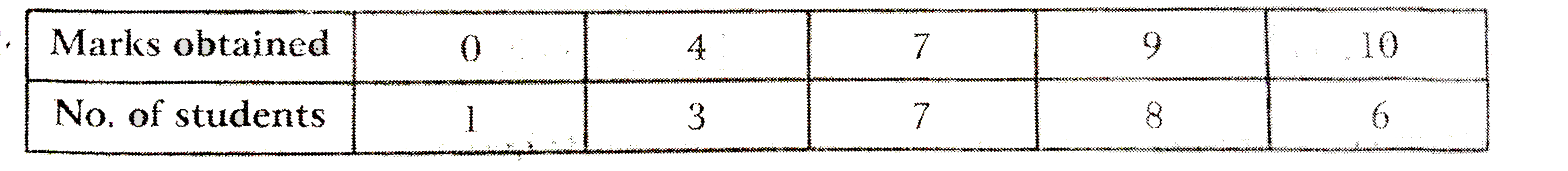 A7.72B7.65C7.4D7
A7.72B7.65C7.4D7In each of the questions given below use the following notations :
A" B means add B to A.
A-B means subtract B from A .
A @ B means divide B by A .
A∗B means multiply by A
In a semester system of examination , the total marks obtained is arrived at the adding 10% of the marks obtained in first periodical , 15% of the marks obtained in the second periodical and 75% of the marks obtained in the final examination . If a student secures P marks out of 150 in the first semester , T marks out of 180 in second semester and M marks out of 400 in the final examination , which of the following will represent the total marks obtained by him ?A(P@150 ∗ 10) '' (T @ 400 ∗ 15)'' (M@ 180 ∗ 75)B(P@ 150∗10)'' (T @ 180∗ 15)'' (M@ 400 ∗75)C(P∗150∗10)'' (T∗ 180 @15)'' (M∗400 75)D(P@ 10∗10)'' (T@180 ∗15)'' (M@ 400∗75)The marks (maximum marks 100) obtained by 20 students in a test are given below :

Find the mean marks of the 20 students.A64B64.5C54D54.5
60 students of Section A of Class XI, obtained 40 mean marks in Statistics, 40 students of Section B obtained 35 mean marks in Statistics. Find out mean marks in Statistics for Class XI as a whole.
View SolutionIf for somex∈R, the frequency distribution of the marks obtained by 20 students in a test is:

Then the mean of the marks is:
View SolutionFollowing are the marks obtained by 20 students in statistics. Find out coefficient of variation of the marks.
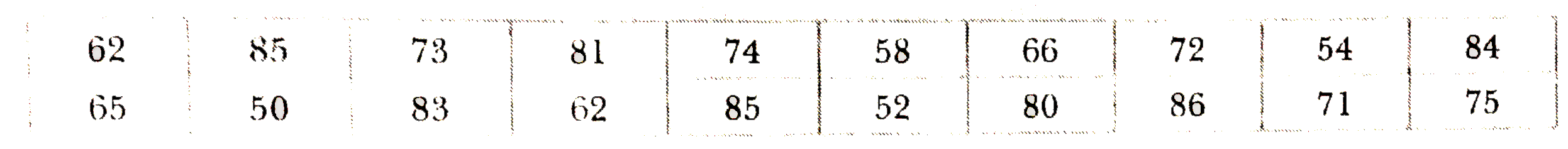
View SolutionThe frequency distribution of the marks obtained by 28 students in a test carrying 40 marks is given below :

If the mean of the above data is 20 , then find the difference between x and y .
View SolutionIn a class test, a student scored 22 marks out of 25 marks . The student 's marks in percentage, is
View Solution

