The heat dissipated across a resistenace R and 10 V is 20 joules per second. The value of R is
3Ω
4Ω
5Ω
8Ω
The correct Answer is:C
To find the value of resistance R given that the heat dissipated across it is 20 joules per second when a voltage of 10 V is applied, we can use the following steps:
1. Understand the Given Information:
- Heat dissipated H=20 joules per second (which is equivalent to watts).
- Voltage E=10 volts.
2. Use the Formula for Heat Dissipated:
The formula for heat dissipated across a resistor is given by:
H=I2R
where I is the current flowing through the resistance R.
3. Apply Ohm's Law:
According to Ohm's Law:
E=IR
Rearranging gives:
I=ER
4. Substitute I in the Heat Formula:
Substitute I from Ohm's Law into the heat formula:
H=(ER)2R
This simplifies to:
H=E2R
5. Rearranging the Formula:
Rearranging the equation to solve for R:
R=E2H
6. Substituting the Values:
Now substitute the known values into the equation:
R=10220=10020=5ohms
Final Answer:
The value of the resistance R is 5ohms.
---
- Heat dissipated H=20 joules per second (which is equivalent to watts).
- Voltage E=10 volts.
The formula for heat dissipated across a resistor is given by:
H=I2R
where I is the current flowing through the resistance R.
According to Ohm's Law:
E=IR
Rearranging gives:
I=ER
Substitute I from Ohm's Law into the heat formula:
H=(ER)2R
This simplifies to:
H=E2R
Rearranging the equation to solve for R:
R=E2H
Now substitute the known values into the equation:
R=10220=10020=5ohms
The value of the resistance R is 5ohms.
Topper's Solved these Questions
- HEATING AND MAGNETIC EFFECTS OF CURRENT Book:MCGROW HILL PUBLICATIONChapter:HEATING AND MAGNETIC EFFECTS OF CURRENT Exercise:HIGHER ORDER THINKING QUESTIONS
Explore 34 Videos
- HEATBook:MCGROW HILL PUBLICATIONChapter:HEATExercise:HIGHER ORDER THINKING QUESTIONS
Explore 15 Videos
- LAWS OF MOTION, FRICTION AND ARCHIMEDES' PRINCIPLEBook:MCGROW HILL PUBLICATIONChapter:LAWS OF MOTION, FRICTION AND ARCHIMEDES' PRINCIPLEExercise:HIGHER ORDER THINKING QUESTIONS
Explore 34 Videos
Similar Questions
Heat dissipation across a resistance R is 500J, if 1.5 A is passed through resistance for 20s what will be heat generation if 3A current is passed across the same resistance for 20 sec
View SolutionA shortage battey with an emf of 10V and an internal resistance 1Ω is connected across an extenal resistance R and liberates of 9W power. Find the potential difference across the teminals of the battery and the value or values of R.
View Solution
Knowledge Check
The power dissipated across resistance R which is connected across a battery of potential V is P. If resistance is doubled, then the power becomes
A1/2B2C1/4D1A 100V voltmeter having an internal resistance of 20kΩ is connected in series with a large resistance R across a 110V line. What is the magnitude of resistance R if the voltmeter reads 5V?
A210kΩB315kΩC420kΩD440kΩA capacitors C1 is charged to a potential V and connected to another capacitor in seris with a resistor R as shown. It is observed that heat H1 is dissipated across resistance R, tilll the circuit reaches steady state. Same process is repeated using resistance of 2R. If H2 is heat dissipated in this case then
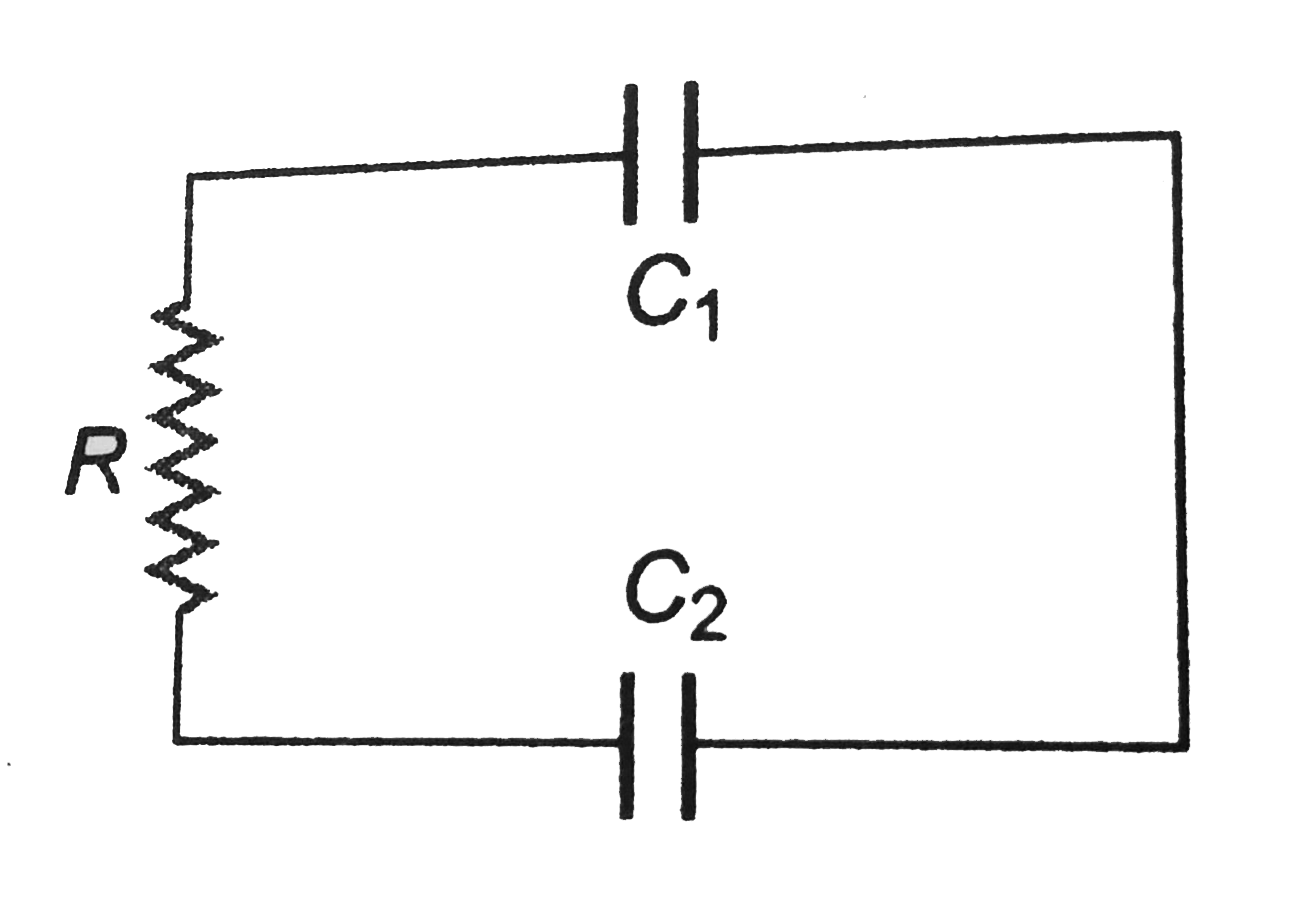 AH2H1=1BH2H1=4CH2H1=14DH2H1=2
AH2H1=1BH2H1=4CH2H1=14DH2H1=2
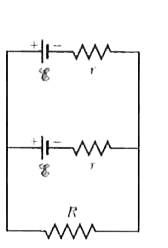
In Fig. 27-38, two batteries with an emf ε=12.0V and an internal resistance r=0.500 Ω are connected in parallel across a resistance R. (a) For what value of R is the dissipation rate in the resistor a maximum? (b) What is that maximum? and (c) what is the total dissipation rate in the batteries? In terms of r, what are (d) the effective R (internal) resistance of the two-battery system and (e) the resistance R that is required to maximize the dissipation rate? This is a general result.
View SolutionFor a CE transistor amplifier the audio signal voltage across the collector resistance of 2.0 kω is 2.0 V suppose the current amplification factor of the transistor is 100 what should be the value of RB in series with VBB 10 times the signal current also calculate the DC drop across the collector resistance
View SolutionA constant voltage is applied to a series R−L circuit by closing the switch. The voltage across inductor (L=2H) is 20V at t=0 and drops of 5V and 20ms. The value of R in Ω is
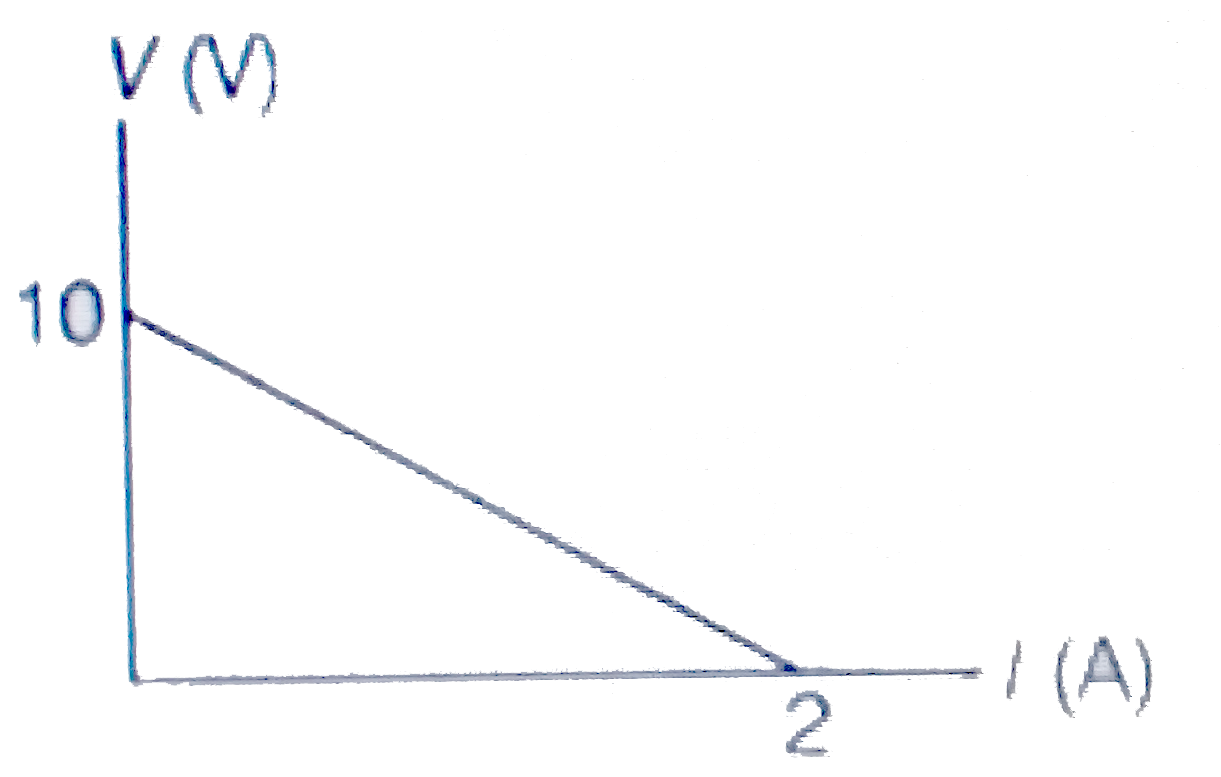
View SolutionA battery of emf E and internal resistance r is connected across a resistance R. Resistance R can be adjusted to any value greater than or equal to zero. A graph is plotted between the current passing through the resistance (I) and potential difference across the termainals of the battery (V). Maximum power developed across the resistance R is
View SolutionThree equal resistace, each of R ohm, are connectedd as shown in the figure. A battery of 2V and of internal resistance 0.1 ohm is connected across the circuit. The value of R for which the heat generated in the circuit maximum will be
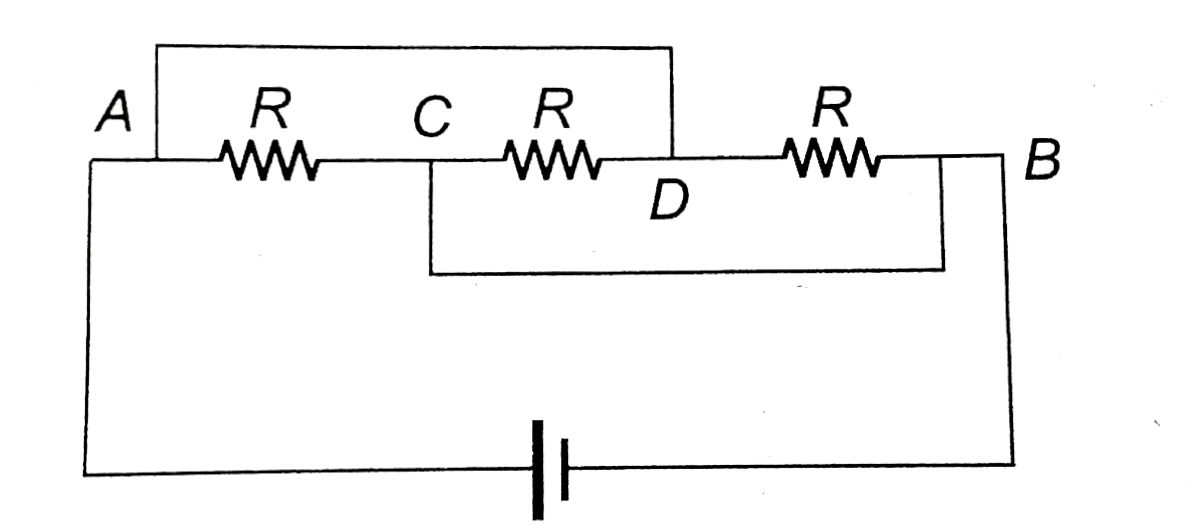
View Solution

