An object is placed in front of a spherical mirror of focal length f. If x and x' recpectively represent the distance of the object and the image from the focus, then
f=x+x'
f2=xx
f=|x−x'|
f=xx
The correct Answer is:B
To derive the relationship between the distances of the object and the image from the focus of a spherical mirror, we can follow these steps:
1. Understand the Mirror Formula:
The mirror formula is given by:
1v+1u=1f
where v is the image distance, u is the object distance, and f is the focal length of the mirror.
2. Define Distances from the Focus:
Let x be the distance of the object from the focus, and x′ be the distance of the image from the focus. Thus, we can express:
u=x+f(since object distance is measured from the mirror)
v=x′+f(since image distance is also measured from the mirror)
3. Substitute into the Mirror Formula:
Substitute u and v into the mirror formula:
1x′+f+1x+f=1f
4. Multiply through by (x′+f)(x+f)f:
To eliminate the fractions, multiply through by (x′+f)(x+f)f:
f(x+f)+f(x′+f)=(x′+f)(x+f)
5. Expand the Equation:
Expanding both sides gives:
fx+f2+fx′+f2=x′x+fx+fx′+f2
6. Simplify the Equation:
Cancel out the common terms on both sides:
f2=x′x−fx−fx′
7. Rearranging the Terms:
Rearranging gives:
x⋅x′=f2+fx+fx′
8. Final Relation:
Thus, we arrive at the relationship:
x⋅x′=f2
Conclusion:
The derived relationship between the distances of the object and the image from the focus of a spherical mirror is:
x⋅x′=f2
The mirror formula is given by:
1v+1u=1f
where v is the image distance, u is the object distance, and f is the focal length of the mirror.
Let x be the distance of the object from the focus, and x′ be the distance of the image from the focus. Thus, we can express:
u=x+f(since object distance is measured from the mirror)
v=x′+f(since image distance is also measured from the mirror)
Substitute u and v into the mirror formula:
1x′+f+1x+f=1f
To eliminate the fractions, multiply through by (x′+f)(x+f)f:
f(x+f)+f(x′+f)=(x′+f)(x+f)
Expanding both sides gives:
fx+f2+fx′+f2=x′x+fx+fx′+f2
Cancel out the common terms on both sides:
f2=x′x−fx−fx′
Rearranging gives:
x⋅x′=f2+fx+fx′
Thus, we arrive at the relationship:
x⋅x′=f2
The derived relationship between the distances of the object and the image from the focus of a spherical mirror is:
x⋅x′=f2
Topper's Solved these Questions
- OPTICSBook:MTG GUIDEChapter:OPTICSExercise:Check your NEET vitals
Explore 25 Videos
- OPTICSBook:MTG GUIDEChapter:OPTICSExercise:AIPMT/NEET
Explore 55 Videos
- OPTICSBook:MTG GUIDEChapter:OPTICSExercise:AIPMT/NEET
Explore 55 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:MTG GUIDEChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:AIPMT/NEET (MCQs)
Explore 48 Videos
Similar Questions
An object is placed in front of a concave mirror of focal length 20 cm. The image formed is three times the size of the object. Calculate two possible distances of the object from the mirror?
View SolutionAn object is placed in front of the concave mirror of focal length f. The magnification of the image became twice when the object distance is changed from 20 cm to 11 cm. Calculate the value of f.
View Solution
Knowledge Check
An object is placed in front of a concave mirror of focal length f as shown in figure. Choose the correct shape of the image.
 A
A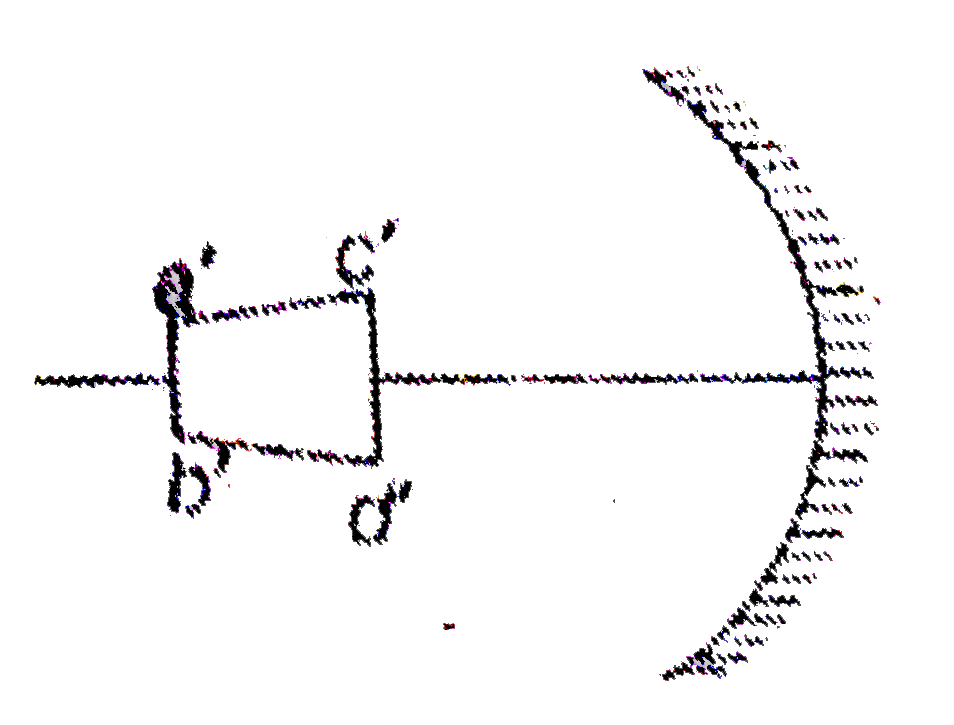 B
B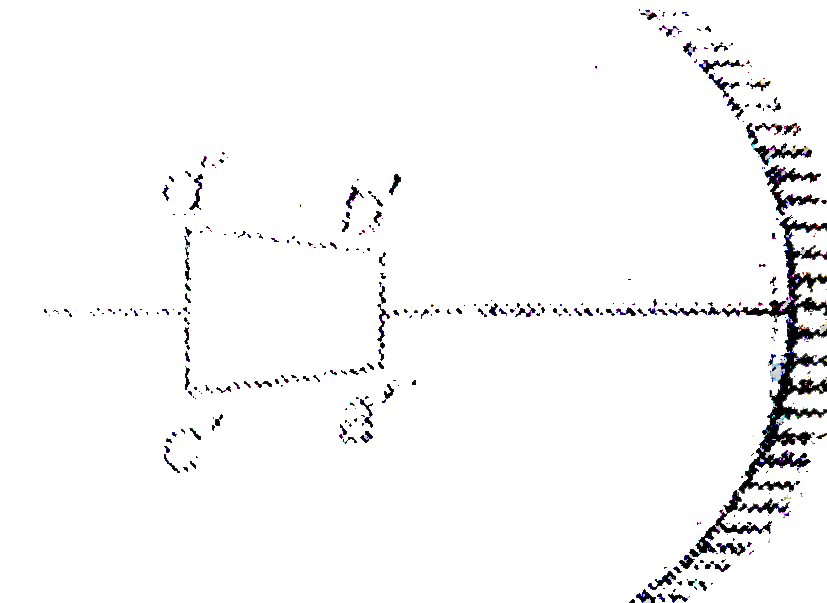 C
C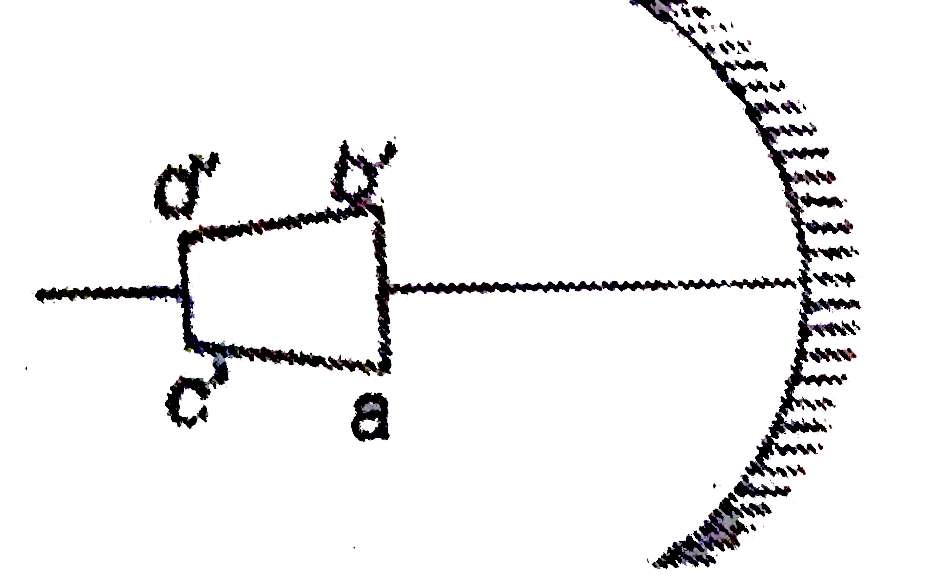 D
D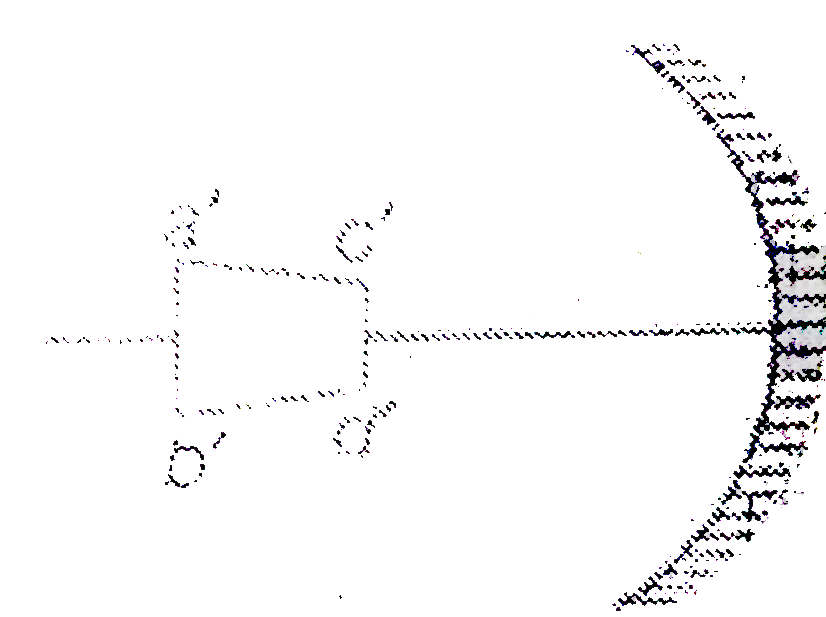
An object is placed in from of a convex mirror of focal length 50 cm, if the image is one fourth the size of the object, the distance of the image from the mirror is
A25 cmB37.5 cmC50 cmD75 cmAn object is placed infront of a convex mirror of focal length f. Find the maximum and minimum distance of two object from the mirror such that the image is real and magnified.
A20and∞Bf and 2fCf and 0DNone of these
A concave mirror of focal length 'f' forms an erect image twice the size of an object. Find the object distance from the mirror.
View SolutionAn object is placed in front of a concave mirror of focal length 20 cm. The image formed is three times the size of the object. Calculate two possible distances of the object from the mirror?
View SolutionAn object is placed 10 cm in front of a convex mirror of focal length 20 cm . The distance of the image from the mirror is
View SolutionAn object is placed at 50 cm in front of a concave mirror of focal length 25 cm. What is the nature of the image produced by the mirror ?
View SolutionAn object is placed in front of a convex mirror at a distance equal to the focal length of the mirror. If its focal length is 20 cm, the distance of the image from the mirror is ______ cm
View Solution

