A ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
50∘
60∘
90∘
40∘
The correct Answer is:C
Reftraction at P,
sin60∘sinr1=√3
sinr1=12
or r1=30∘
Since, r2=r1,∴r2=30∘
Refraction at Q, sinr2sini2=1√3 or sin30∘sini2=1√3
or i2=60∘
At point Q, r.2=r2=30∘
∴α=180∘−(r.2=r2)=180∘−(30∘+60∘)=90∘ 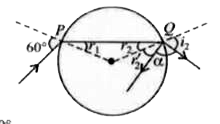
Topper's Solved these Questions
- OPTICSBook:MTG GUIDEChapter:OPTICSExercise:Check your NEET vitals
Explore 25 Videos
- OPTICSBook:MTG GUIDEChapter:OPTICSExercise:AIPMT/NEET
Explore 55 Videos
- OPTICSBook:MTG GUIDEChapter:OPTICSExercise:AIPMT/NEET
Explore 55 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:MTG GUIDEChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:AIPMT/NEET (MCQs)
Explore 48 Videos
Similar Questions
A ray of light-is incident on glass at the polarising angle ip. Find the angle between the reflected and refracted rays.
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View Solution
Knowledge Check
A ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
A120∘B90∘C60∘D150∘A ray R1 is incident on the plane surface of the glass slab (kept in air) of refractive index √2 at angle of incident equal to the critical angle for this air glass system. The refracted ray R2 undergoes partial reflection & refraction at the other surface. The angle between the reflected ray R3 and the refracted ray R4 at that surface is :
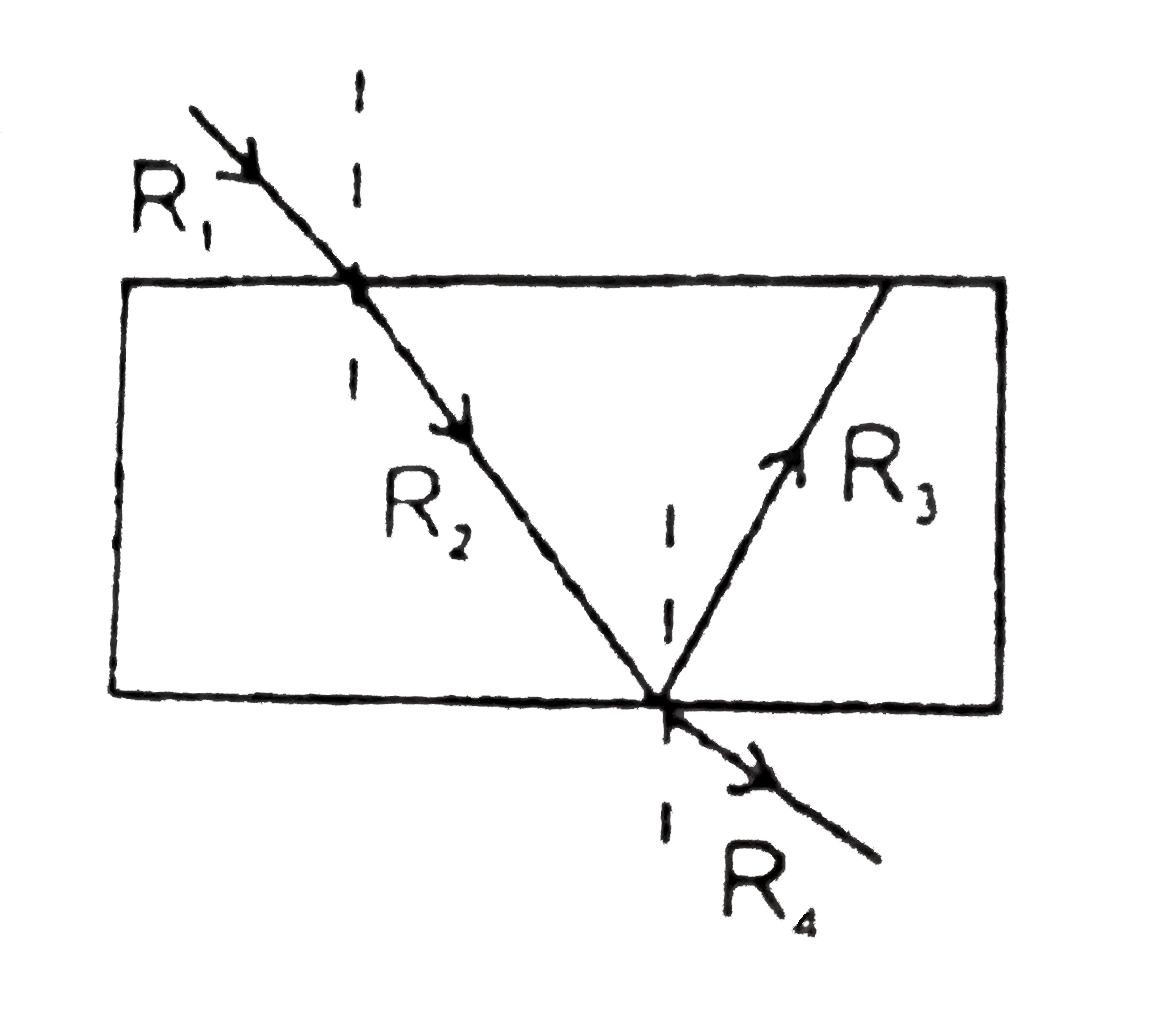 A45∘B135∘C105∘D75∘
A45∘B135∘C105∘D75∘The angle between incident ray and reflected ray or refracted ray is called _____
Arespective angle of deviationBangle of minimum deviationCglancing angleDemergence angle
The angle of incidence on the surface of a diamond of refractive index 2.4, if the angle between the reflected and refracted rays is 90° is
View SolutionA ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle ϕ. If μ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
View SolutionA ray of light strikes a tansparent rectangular slab (of refractive index √2) At an angle of incidence of 45∘. The angle between the reflected and refracted rays is
View SolutionA ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle between the reflected and refracted rays is
View SolutionA ray of light in incident on a glass plate at an angle of 60∘. What is the refractive index of glass if the reflected and refracted rays are perpendicular to each other?
View Solution

