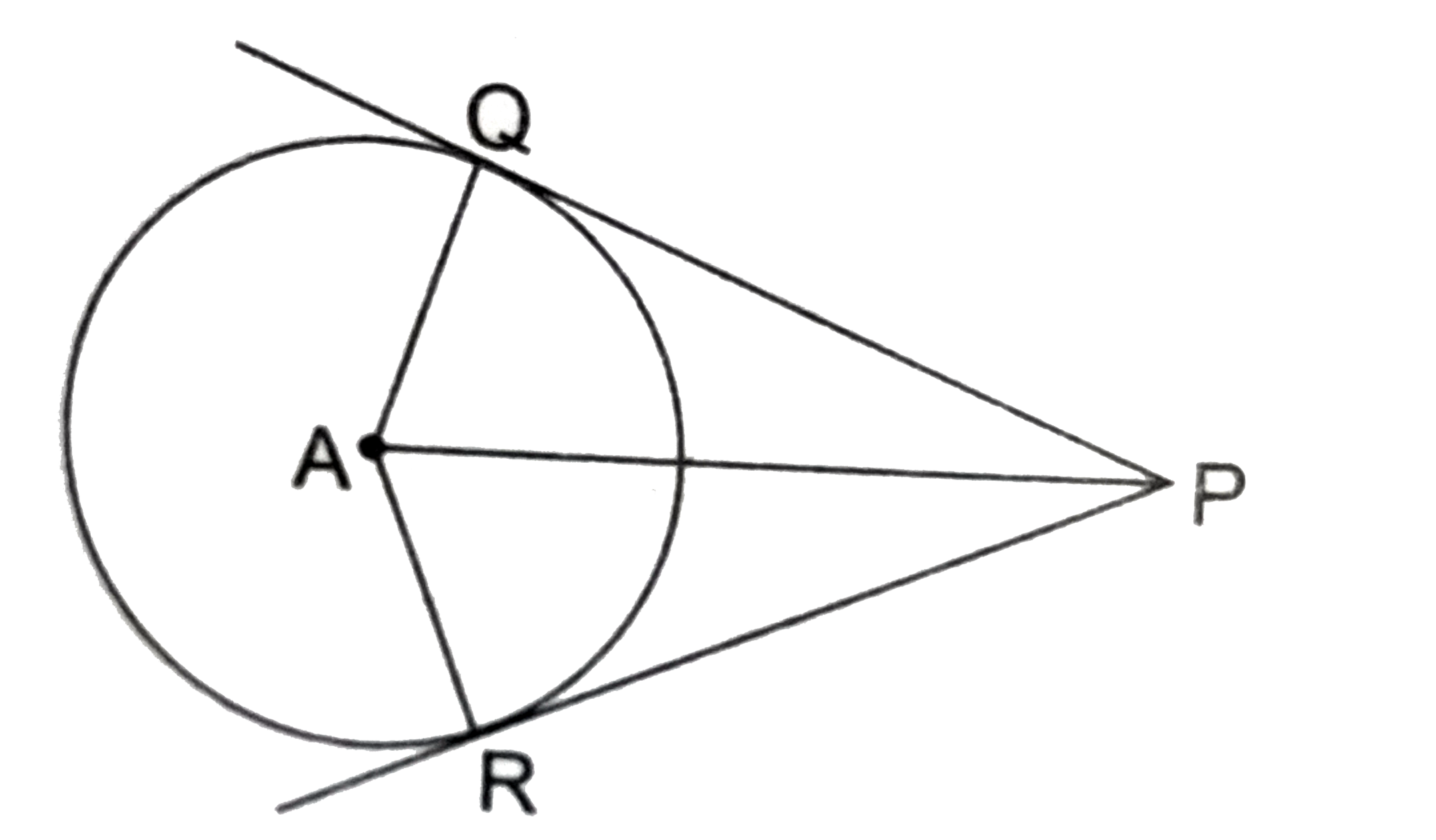
In the given figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27∘ then ∠QAR equals
A
63∘
B
117∘
C
126∘
D
153∘
Video Solution
Text Solution
∠QPR=2∠QPA=2×27∘=54∘[∵AP bisect ∠QPR]
Now,QPRA is a cyclic quadrilateral
⇒∠QAR+∠QPR=180∘
⇒∠QAR=180∘−54∘=126∘.
|
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Assertion-and-Reason
1 Video
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Test Yourself
20 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)
15 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
Knowledge Check
If PQ and PR be the two tangents to a circle with centre O such that ∠QPR=120∘ then ∠POQ is
A90∘B45∘C30∘D60∘If PQ and PR are two tangents to ta circle with centre O. if ∠QPR=46∘, then ∠QOR is equal to
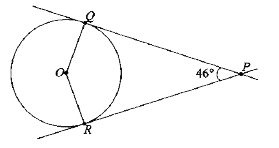 A67∘B46∘C44∘D134∘
A67∘B46∘C44∘D134∘In the figure , PQ and PR are the tangents drawn form P to a circle with centre O. if ∠OPQ=35∘ then
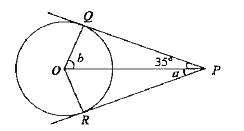 Aa=30∘,b=60∘Ba=35∘,b=55∘Ca=40∘,b=50∘Da=45∘,b=45∘
Aa=30∘,b=60∘Ba=35∘,b=55∘Ca=40∘,b=50∘Da=45∘,b=45∘
In Fig. 10.101, PQ and PR are two tangents to a circle with centre O . If ∠QPR=46o , then ∠QOR equals (FIGURE) 67o (b) 134o (c) 44o (d) 46o
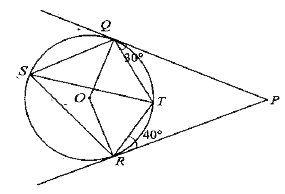
View SolutionIn the figures, PQ and PR are tangents to the circle with centre O. Find RSQ , RTQ , and RˆPQ
View SolutionIn the given figure, PQ is tangent at a point R of the circle with centre O. If , find m∠PRS.
View SolutionIn the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
View SolutionIf PQ and PR be the two tangents to a circle with centre O such that ∠QPR=120∘ then ∠POQ is
View Solution
