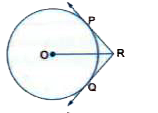
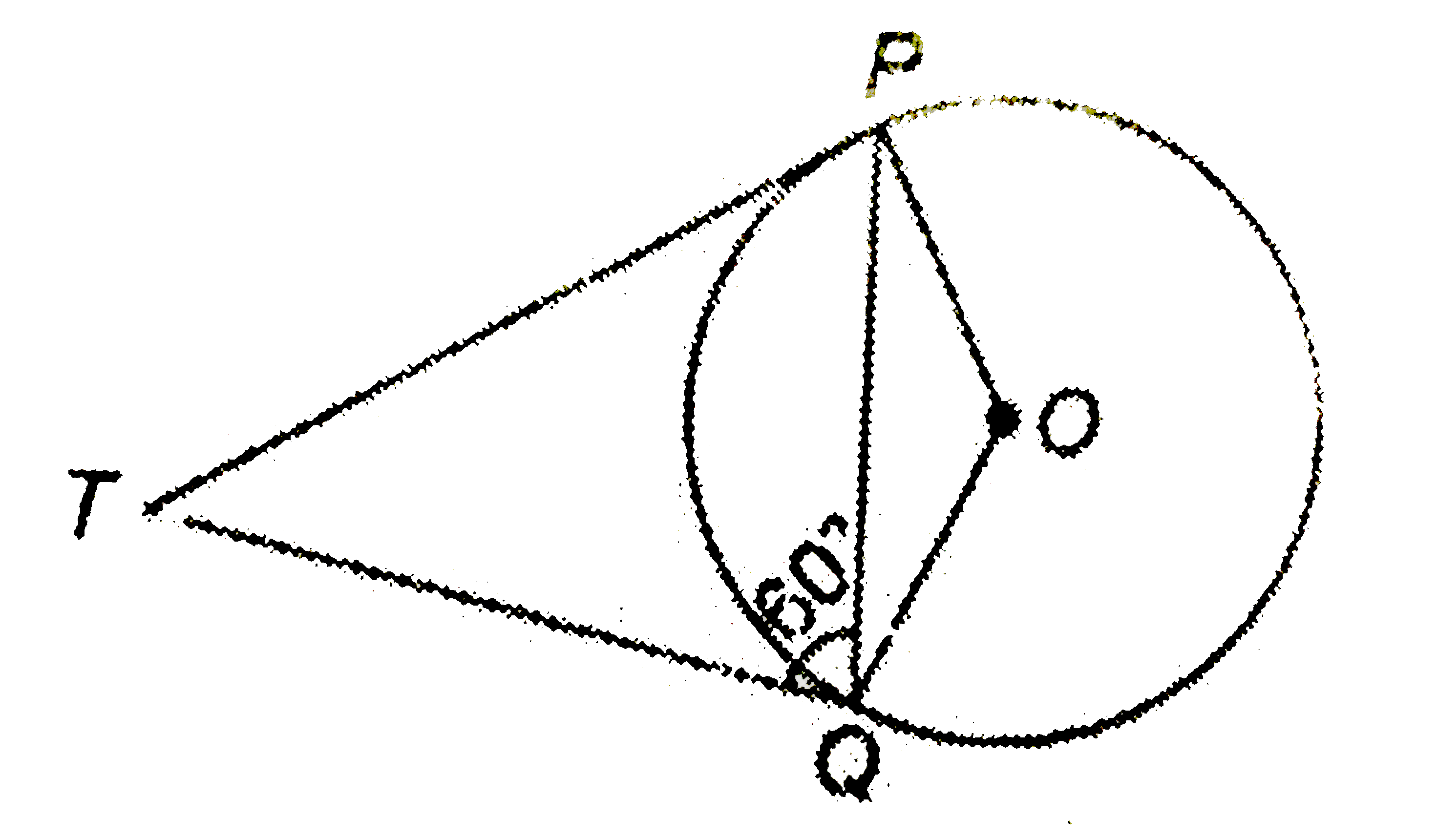
In the given figure, two tangents RQ and RP are drwn from an external point R to the circle with centre O. If ∠PRQ=120∘, then prove that OR=PR+RQ.
Video Solution
Text Solution
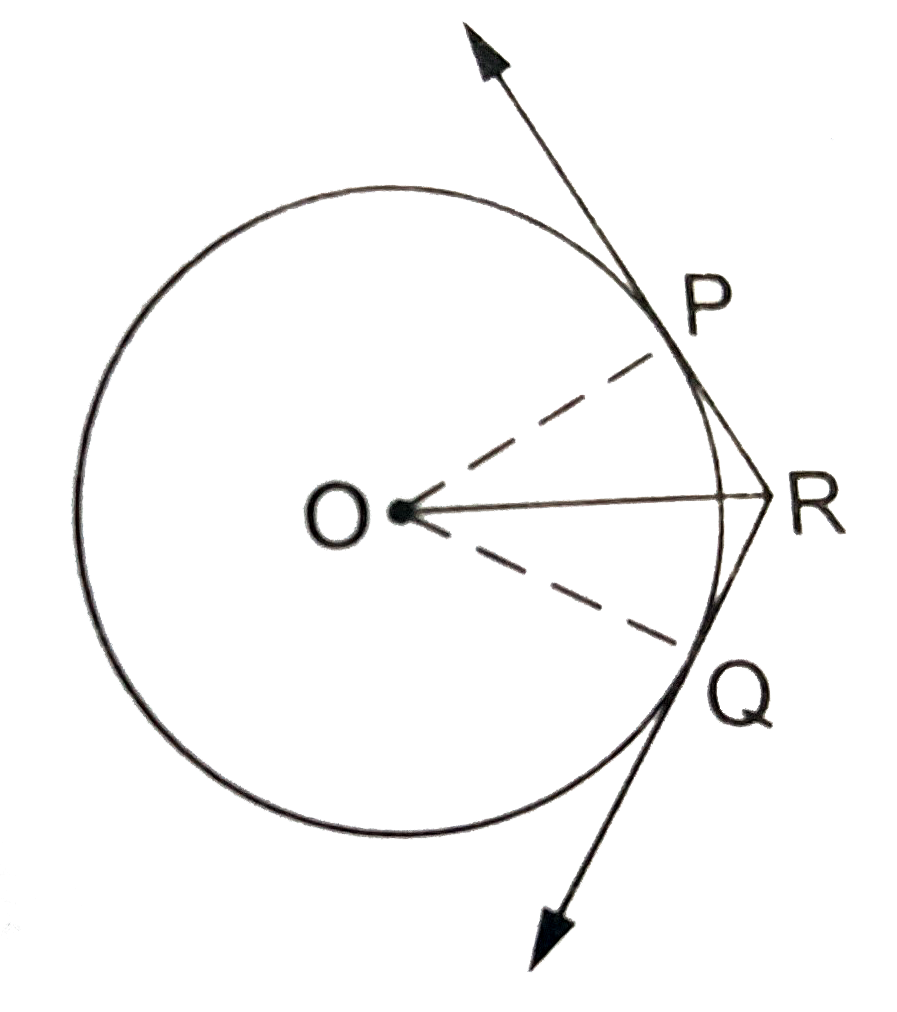
Join OP and OQ.
∠PRQ=120∘⇒∠PRO=∠QRO=12×∠PRQ=60∘. [∵ two tangents from an external point are equally inclined to the line segement joining the centre to that point. And so, ∠PRO=∠QRO=12∠PRQ.
In right ΔOPR, we have
cos=∠PRO=PROR⇒cos60∘=PROR⇒12=PROR⇒PR=12×OR.
Similarly, RQ=12×OR.
∴PR+RQ=OR.
|
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)
15 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple-choice questions (MCQ)
39 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A
16 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
Knowledge Check
In the given figure tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPO=30∘. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
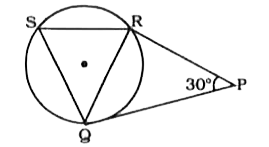 A30∘B50∘C45∘D60∘
A30∘B50∘C45∘D60∘In the figure, PA is a tangent from an external point P to the circle with centre O and diameter AB. If ∠POB=110∘, then the measure of ∠APO is:
A40∘B20∘C25∘D30∘In the figure , if TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP=60∘, then ∠OPQ =
 A25∘B60∘C40∘D30∘
A25∘B60∘C40∘D30∘
In the given figure, two tangents PQ and PR are drawn to a circle with centre C from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionIn the given figure, TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP=60∘. Find angelOPQ.
View SolutionIn the figure, PA is a tangent from an external point P to a circle with centre O. If ∠POB=115∘, find ∠APO.

View SolutionProve that the lengths of tangents drawn from an external point to a circle are equal.
View SolutionIn the given figure, PQ is tangent at a point R of the circle with centre O. If , find m∠PRS.
View Solution