In figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ=70∘, find ∠TRQ.
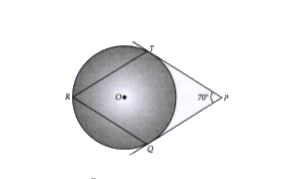
Join OT and OQ.
Then, ∠TOQ+∠TPQ=180∘⇒∠TOQ=180∘−70∘=110∘
Now, /TRQ=1∘×∠TOQ=12×110∘=55∘ [∵ the angle subtended by an arc of a circle at the centre is double the angle subtended by it any point on the remaining part of the circle.]
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)
15 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple-choice questions (MCQ)
39 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A
16 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT=30∘, prove that BA:AT =2:1
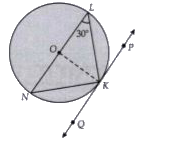
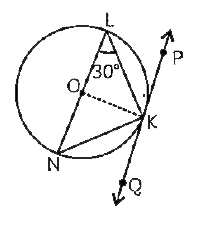
View SolutionIn given figure, O is the centre of the circle and LN is a diameter. If PQ is a tangent to the circle at K and ∠KLN=30∘, find ∠PKL.
View Solution
Knowledge Check
Two tangents PA and PB are drawn to a circle with centre O from an external point P. If ∠OAB=30∘, then ∠APB is:
केंद्र O वाले वृत्त पर एक बाहरी बिंदु P से दो स्पर्श रेखाएँ PA तथा PB खींची जाती हैं | यदि ∠OAB=30∘ है, तो ∠APB का मान क्या होगा ?A15∘B30∘C120∘D60∘
In the figure, O is the centre of the circle and LN is a diameter. If PQ is a tangent to the circle at K and ∠KLN=30∘, find ∠PKL.
View SolutionIn Figure 4, PQ and PR are tangents drawn to a circle with centre O from an external point P. If ∠PRQ=70∘, then find ∠QPRand∠OQR
View SolutionIn Figure, O is the centre of a circle and PQ is a diameter. If ∠ROS=400, find ∠RTS
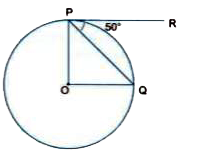
View SolutionIn Fig , O is the centre of a circle , PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ. Find ∠POQ .
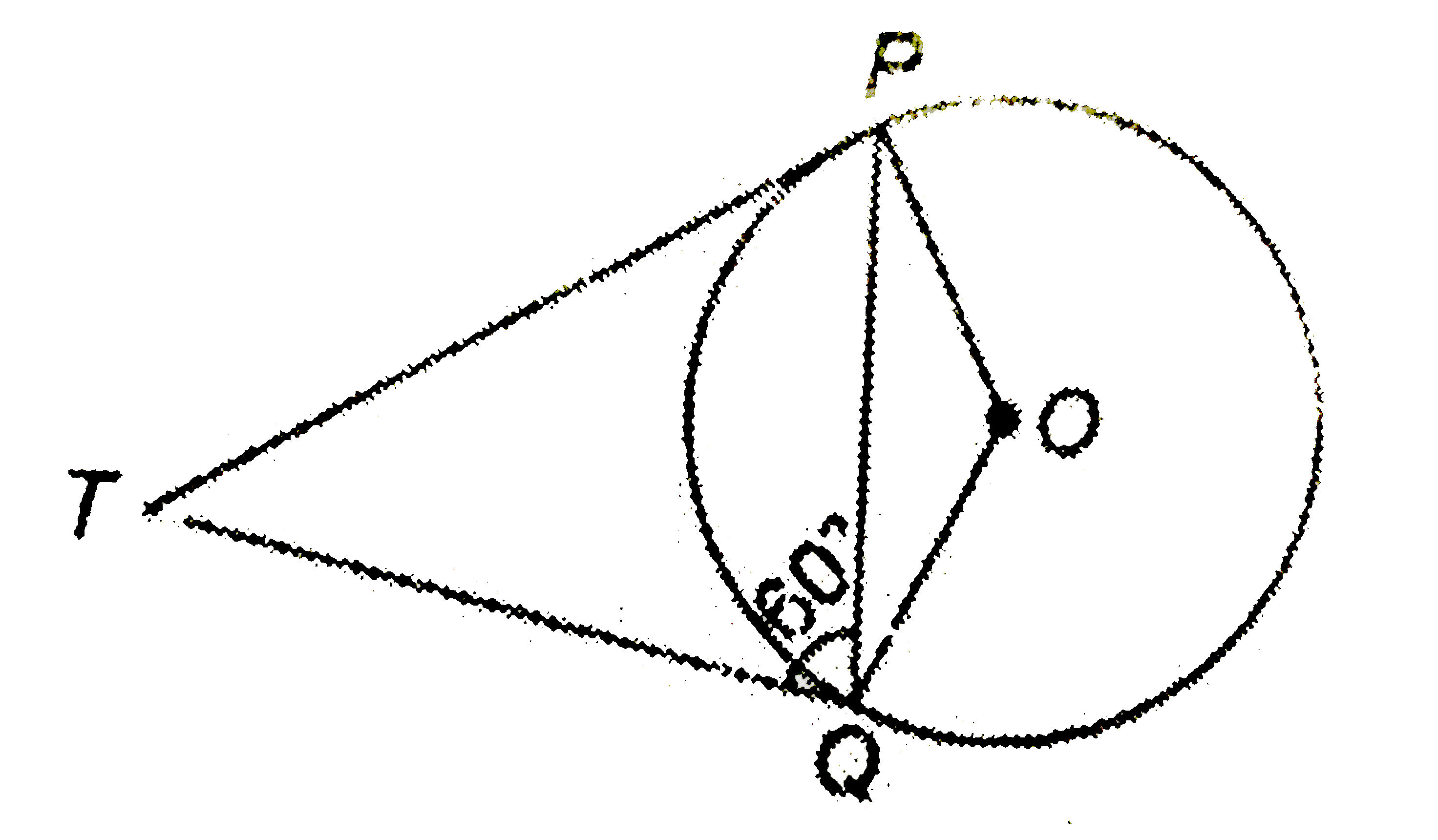
View SolutionIn the given figure, TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP=60∘. Find angelOPQ.
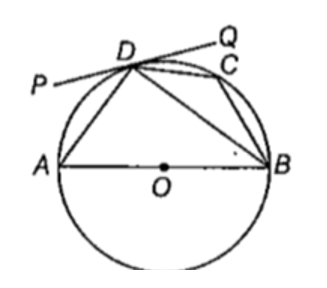
View SolutionIn the adjoning figure O is the centre of the circle and AB is the diameter. Tangent PQ touches the circle at D. ∠BDQ=48∘. Find the ratio of angleDBA:angleDCB.
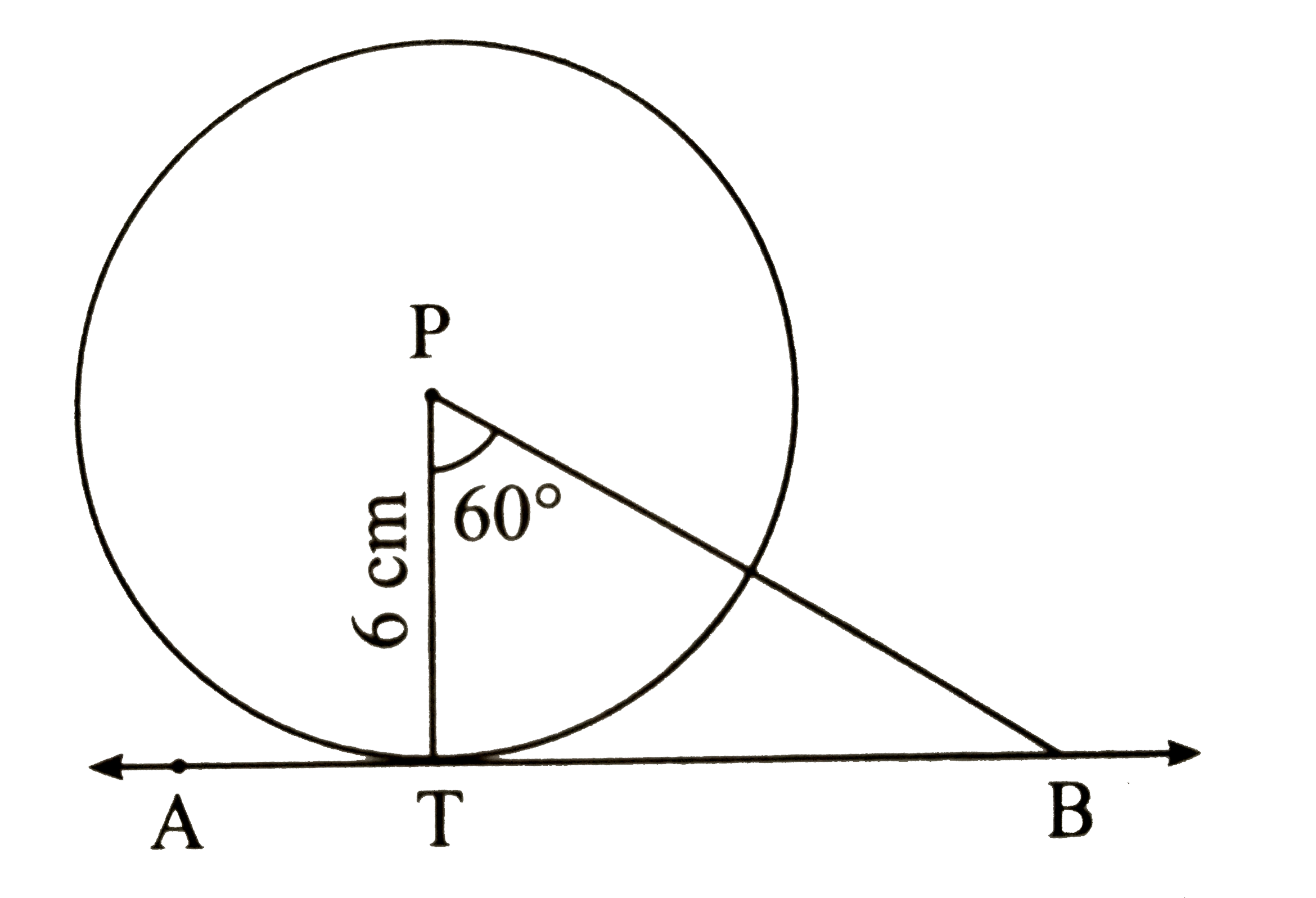
View SolutionIn the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘
View Solution
