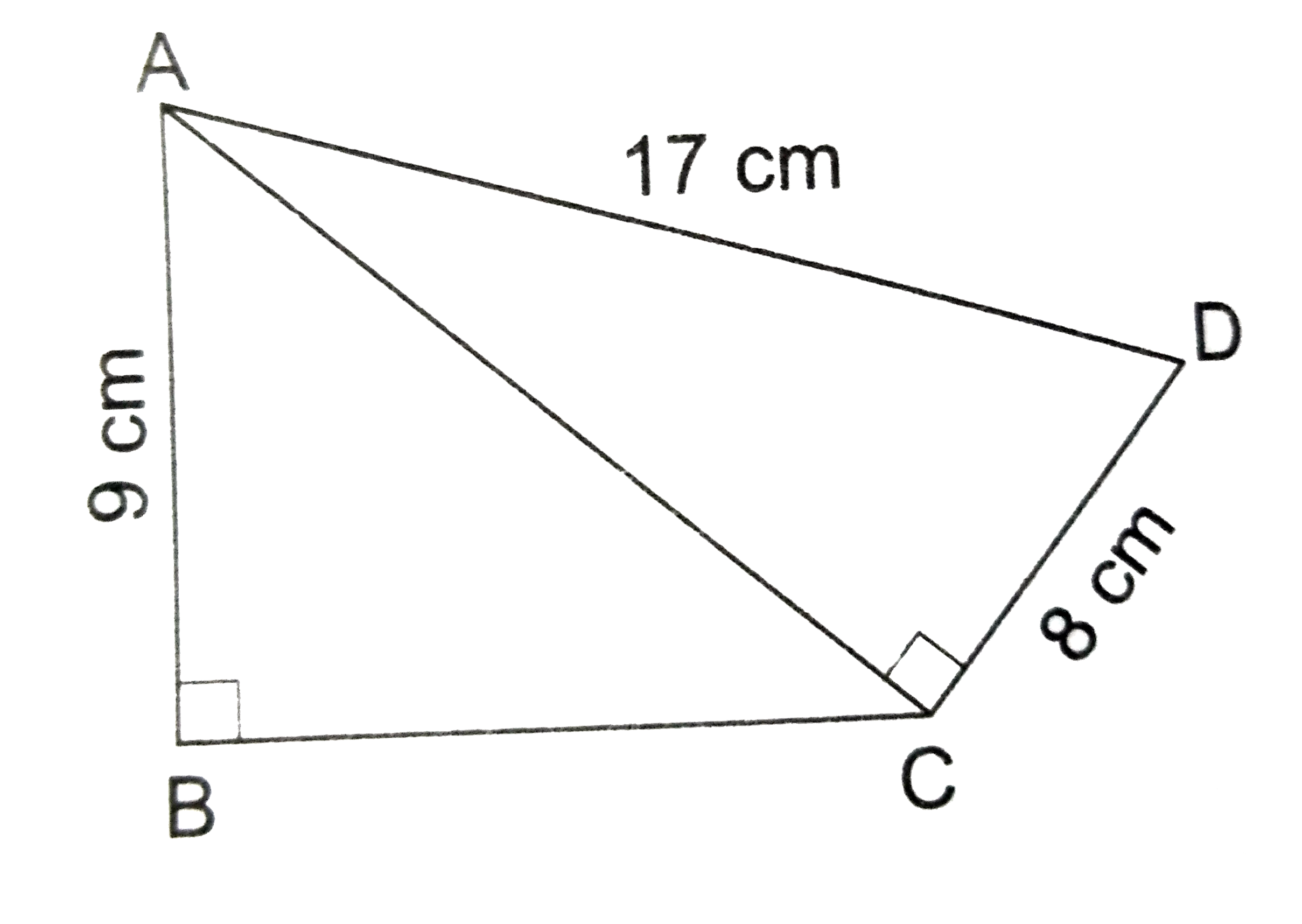
The area of quadrilateral ABCD in the given figure is
A
57cm2
B
108cm2
C
114cm2
D
195cm2
Video Solution
Text Solution
The correct Answer is:C
In right △ACD,AC2=(AD2−CD2)=(17)2=(8)2=(289−64)=225.
∴AC=√225 = 15 cm.
In right △ABC,BC2=AC2−AB2=(15)2=(9)2=(225−81)=144.
∴BC=√144=12cm.
ar(quad. ABCD)=ar(△ACD)+ar(△ABC)
=[12×8×15)+(12×12×9)]cm2=(60+54)cm2=144cm2
|
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
The area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral isA4B2C1Dnone of theseHow to many quadrilaterals are there in the given figure ?
 A2B3C4D5
A2B3C4D5How many quadrilaterals are there in the given figure?
 A13B15C17D19
A13B15C17D19
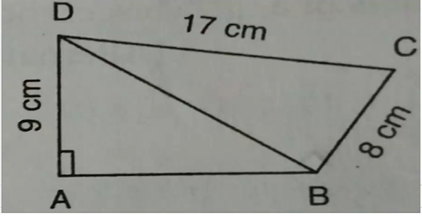
Compute the area of quadrilateral ABCD.

View SolutionIn the given figure, compute the area of quadilateral
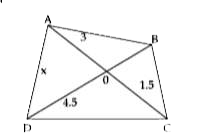
View SolutionIn Quadrilateral ABCD, diagonal AC & BD intersect at "O". By Diagonals area of quadrilateral ABCD is divided into 4 parts. Find area of the fourth part (x), area of other 3 parts is mentioned in the figure.
View SolutionIn the given figure, ABCD is rectangle and EF is perpendicular to AB. The area of the shaded region, in the given figure, is
View SolutionSides AB and CD of a quadrilateral ABCD are extended as in figure. Then a + b is equal to

View Solution
