The side of a parallelogram is produced to any point A line through and parallel to meets produced at and then parallelogram is completed as shown in Figure. Show that
Join AC, CP, PQ and QA.
Now, being on the same base AQ and between the same parallels AQ and CP, we have
[ AC divides ||gm ABCD into two of equal area and QP divides ||gm BQRP into two of equal area]
Hence, .
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES Book:RS AGGARWALChapter:AREAS OF PARALLELOGRAMS AND TRIANGLES Exercise:Exercise 11
Explore 38 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES Book:RS AGGARWALChapter:AREAS OF PARALLELOGRAMS AND TRIANGLES Exercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBook:RS AGGARWALChapter:AREAS OF TRIANGLES AND QUADRILATERALSExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
Similar Questions
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(^(gm)ABCD)=argmPBQR).

View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(∣∣gmABCD)=ar(∣∣gmPBQR)
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that ar (ABCD) = ar (PBQR).
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CP meets CB produced in Q and the parallelogram PBQR completed. Show that ar(^(gm)ABCD)=ar(^(gm)BPRQ). CONSTRUCTION : Join AC and PQ. TO PROVE : ar(^(gm)ABCD)=ar(^(gm)BPRQ)
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
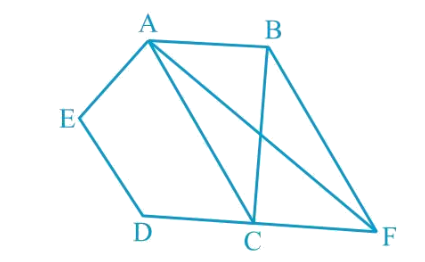
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that ar(ACB)=ar(ACF) (ii) ar(AEDF)=ar(ABCDE)
View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in Figure. Prove that ar (ABP)=ar (Qua..ABCD).
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: ar (ACB)=ar (ACF) ar (AEDF)=ar (ABCDE)
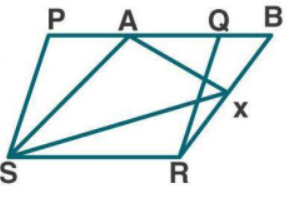
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
View Solution