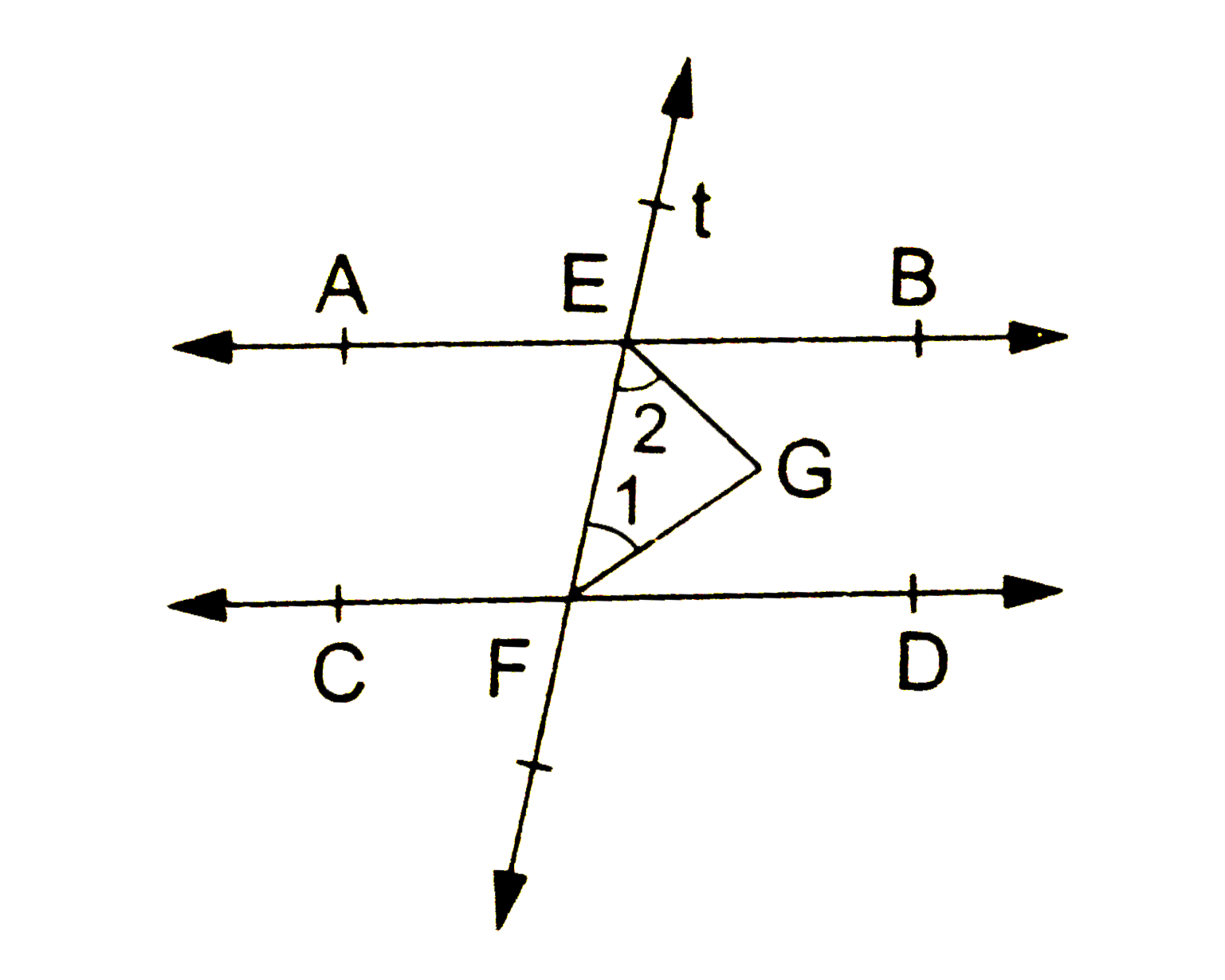
If two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
Given and t is a transversal, cutting them at E and F respectively. Also, EG and FG, the bisectors of respectively, meet at G. TO PROVE
PROOF and t is a transversal.
But in we have
.
Hence, .
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXAMPLE
Explore 10 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 8
Explore 13 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Matching of Columns:
Explore 2 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:RS AGGARWALChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Multiple Choice Questions (Mcq)
Explore 73 Videos
Similar Questions
Knowledge Check
If two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of the transversal is
A1B2C3D4If two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
AequalBadjacentCSupplementaryDComplementaryTwo parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
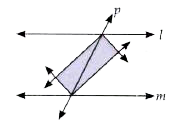 ATrapeziumBKiteCParallelogramDSquare
ATrapeziumBKiteCParallelogramDSquare
If two parallel lines are intersected by a transversal then prove that the bisectors of any pair of alternate interior angles are parallel.
View SolutionIf two parallel lines are intersected by a transversal; the bisector of any two corresponding angles are parallel.
View SolutionIf two lines are intersected by a transversal; the bisectors of any pair of alternate interior angles are parallel.
View SolutionFill in the blanks in each of the following to make the statement true: (i) If two parallel lines are intersected by a transversal, then each pair of corresponding angles are.... (ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are... (iii) Two lines perpendicular to the same line are.... to each other. (iv) Two lines parallel to the same line are .......... to each other. (v) If a transversal intersects a pair of lines in such away that a pair of alternate angles are equal, then the line are... (vi) If a transversal intersects a pair of lines in such away that the sum of interior angles on the same side of transversal is 180,then the line are .......
View SolutionIf two parallel lines intersected by a transversal , then name the pair of angles formed that are equal .
View Solution