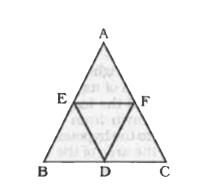
lf D, E and F are respectively the midpoints of the sides BC, CA and AB of an equilateral triangle ABC, prove that △DEF is also an equilateral triangle.
Since D and F are the midpoints of sides BC and CA respectively, we have DE=12AB (by midpoint theorem).
Similarly, FE=12BCandDF=12BCandDF=12CA.
∴AB=BC=CA⇒12AB=12BC=12CA⇒DE=FE=DF.
Thus, all the sides of △DEF are equal .
Hence, △DEF is an equilateral triangle.
Topper's Solved these Questions
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:EXAMPLE
Explore 32 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Exercise 10 A
Explore 10 Videos
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 10 Videos
Similar Questions
lf D, E and F are respectively the midpoints of the sides BC, CA and AB of an equilateral triangle ABC, prove that △DEF is also an equilateral triangle.
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View Solution
Knowledge Check
If D,E and F are respectively the midpoint of the sides BC,CA and AB of a ΔABC and the area of ΔABC=36cm2 , then area of ΔDEF is -----
A12cm2B9cm2C18cm2D8cm2If D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
A1:4B1:2C1:3D2:3
D, E and F are the mid-points of the sides BC, CA and AB, respectively of and equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

View SolutionIf D, E and F are the mid-points of the sides of an equilateral triangle ABC, then the ratio of the area of triangle DEF and DCF is :
View SolutionD, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogram
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View SolutionD, E and F are respectively the mid-points of sides AB. BC and CA of △ABC. Find the ratio of the areas of △DEF and △ABC.
View Solution
