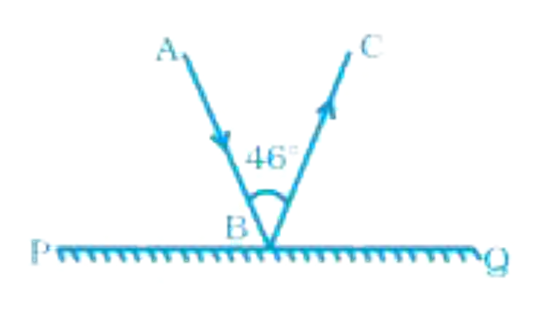
In the given figure, AB is a mirror, PQ is the incident ray and QR is the relfected ray. If ∠PQR=108∘ then ∠AQP=?
A
72∘
B
18∘
C
34∘
D
54∘
Video Solution
Text Solution
The correct Answer is:C
Angle of incidence = angle of reflection =x∘ (say).
Draw QM as normal to AB at Q.
|
Topper's Solved these Questions
- LINES AND ANGLESBook:RS AGGARWALChapter:LINES AND ANGLESExercise:Exercise 7C
Explore 24 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:RS AGGARWALChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Multiple Choice Questions (Mcq)
Explore 24 Videos
- MEAN , MEDIAN AND MODE OF UNGROUPED DATA Book:RS AGGARWALChapter:MEAN , MEDIAN AND MODE OF UNGROUPED DATA Exercise:Multiple Choice Questions (Mcq)
Explore 18 Videos
Similar Questions
Knowledge Check
two supplementary angles are in the ratio 3:2, find the angles.
A108∘,72∘B118∘,72∘C72∘,208∘DNone of theseDuring the reflectio of ligth from plane mirror, the incident ray, normal and reflected ray lie
Aparalel to eacch otherBperpendicular to each otherCin same planeDin different planeThe angle which the incident ray makes with the mirror is called
Aangle of incidenceBangle of reflectionCright angleDglancing angle of incidence
In the given figure, PQ||ABandPR||AC.
Prove that QR∣∣BC
View SolutionWhat is the angle of incidence of a ray if the reflected ray is at an angle of 90∘ to the incident ray?
View SolutionA ray of light falls on a plane mirror. When the mirror is turned, about an axis at right angle to the plane of the mirror through 20∘, the angle between the incident ray and new reflected ray is 45∘. Find the angle between the incident ray and original reflected ray.
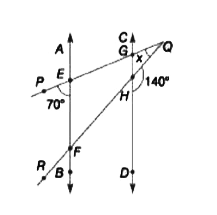
View SolutionIn the figure AB || CD and PQ,QR intersects AB and CD both at E,F, and G,H respectively. If ∠PQR =x, then find the value of x (in degrees).
View SolutionIn triangle PQ=QR,∠QPR=48∘,∠SRP=18∘ then ∠PQR=
View Solution