In triangle PQ=QR,∠QPR=48∘,∠SRP=18∘ then ∠PQR=
48∘
84∘
30∘
36∘
To find the angle PQR in triangle PQR given that PQ = QR, angle QPR = 48°, and angle SRP = 18°, we can follow these steps:
1. Identify the Angles in Triangle PQR:
- We know that PQ = QR, which means triangle PQR is isosceles. Therefore, angle PQR = angle PRQ.
2. Express Angle R in Terms of Angle S:
- Since angle R (angle QRP) can be expressed as the sum of angle QRS and angle SRP, we can write:
Angle QRP=Angle QRS+Angle SRP
- Given that angle SRP = 18°, we can denote angle QRS as x. Thus:
Angle QRP=x+18°
3. Use the Isosceles Triangle Property:
- Since PQ = QR, we have:
Angle PQR=Angle PRQ
- Let angle PQR = angle PRQ = y.
4. Set Up the Equation Using the Triangle Sum Property:
- The sum of the angles in triangle PQR is 180°:
Angle PQR+Angle QRP+Angle RPQ=180°
- Substituting the known values:
y+(x+18°)+48°=180°
- Simplifying this gives:
y+x+66°=180°
- Therefore:
y+x=114°
5. Express Angle R in Terms of Angle P:
- Since angle PQR = angle PRQ (both are y), we can also express angle QRP (angle R) as:
Angle QRP=114°−y
- We know that angle QRP = x + 18° from step 2, so:
x+18°=114°−y
6. Substitute for x:
- From the equation y+x=114°, we can express x as:
x=114°−y
- Substitute this into the equation:
(114°−y)+18°=114°−y
- This simplifies to:
132°−y=114°−y
- Therefore, we can find y:
y=84°
7. Conclusion:
- Thus, angle PQR = 84°.
Final Answer:
Angle PQR=84°
- We know that PQ = QR, which means triangle PQR is isosceles. Therefore, angle PQR = angle PRQ.
- Since angle R (angle QRP) can be expressed as the sum of angle QRS and angle SRP, we can write:
Angle QRP=Angle QRS+Angle SRP
- Given that angle SRP = 18°, we can denote angle QRS as x. Thus:
Angle QRP=x+18°
- Since PQ = QR, we have:
Angle PQR=Angle PRQ
- Let angle PQR = angle PRQ = y.
- The sum of the angles in triangle PQR is 180°:
Angle PQR+Angle QRP+Angle RPQ=180°
- Substituting the known values:
y+(x+18°)+48°=180°
- Simplifying this gives:
y+x+66°=180°
- Therefore:
y+x=114°
- Since angle PQR = angle PRQ (both are y), we can also express angle QRP (angle R) as:
Angle QRP=114°−y
- We know that angle QRP = x + 18° from step 2, so:
x+18°=114°−y
- From the equation y+x=114°, we can express x as:
x=114°−y
- Substitute this into the equation:
(114°−y)+18°=114°−y
- This simplifies to:
132°−y=114°−y
- Therefore, we can find y:
y=84°
- Thus, angle PQR = 84°.
Angle PQR=84°
Topper's Solved these Questions
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-2 )
10 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Multiple Choice Questions) (MATCH THE FOLLOWING)
2 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.5)
4 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
In right-angled triangle PQR, if ∠P=60∘,∠R=30∘andPR =12, then find the values of PQ and QR.
View SolutionIn △PQR, ∠Q=84∘,∠R=48∘, PS⊥QR at S and the bisector of ∠P meet QR at T. What is a measure of ∠SPT?
△PQR में,∠Q=84∘,∠R=48∘, PS⊥QR और ∠P का द्विभाजक QR से T पर मिलता है ∠SPT का मान क्या होगा ?
View Solution
Knowledge Check
In a triangle PQR, let ∠PQR=30∘ and the sides PQ and QR have lengths 10√3 and 10, respectively. Then, which of the following statement(s) is (are) TRUE ?
A∠QPR=45∘BThe area of the triangle PQR is 25√3and∠QRP=120∘CThe radius of the incircle of the triangle PQR is 10√3−15DThe area of the circumcircle of the triangle PQR is 100πIn ΔPQT,PQ=PT . The points R and S are on QT such that PR = PS . If ∠PTS=62∘and∠RPS=34∘ then measure of ∠QPR is
A11∘B13∘C15∘D17∘In a triangle PQR,∠Q=90∘. If PQ=12cm and QR=5 cm, then what is the radius ( in cm ) of the circumcircle of the triangle ?
A5B6C6.5D6√2
In the figure , AB∣∣CD and PQ,QR intersect AB and CD both at E, F G and H respectively. Given that ∠PEB=80∘,∠QHD=120∘ and ∠PQR=x, then find the value of x .
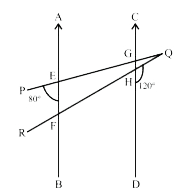
View Solution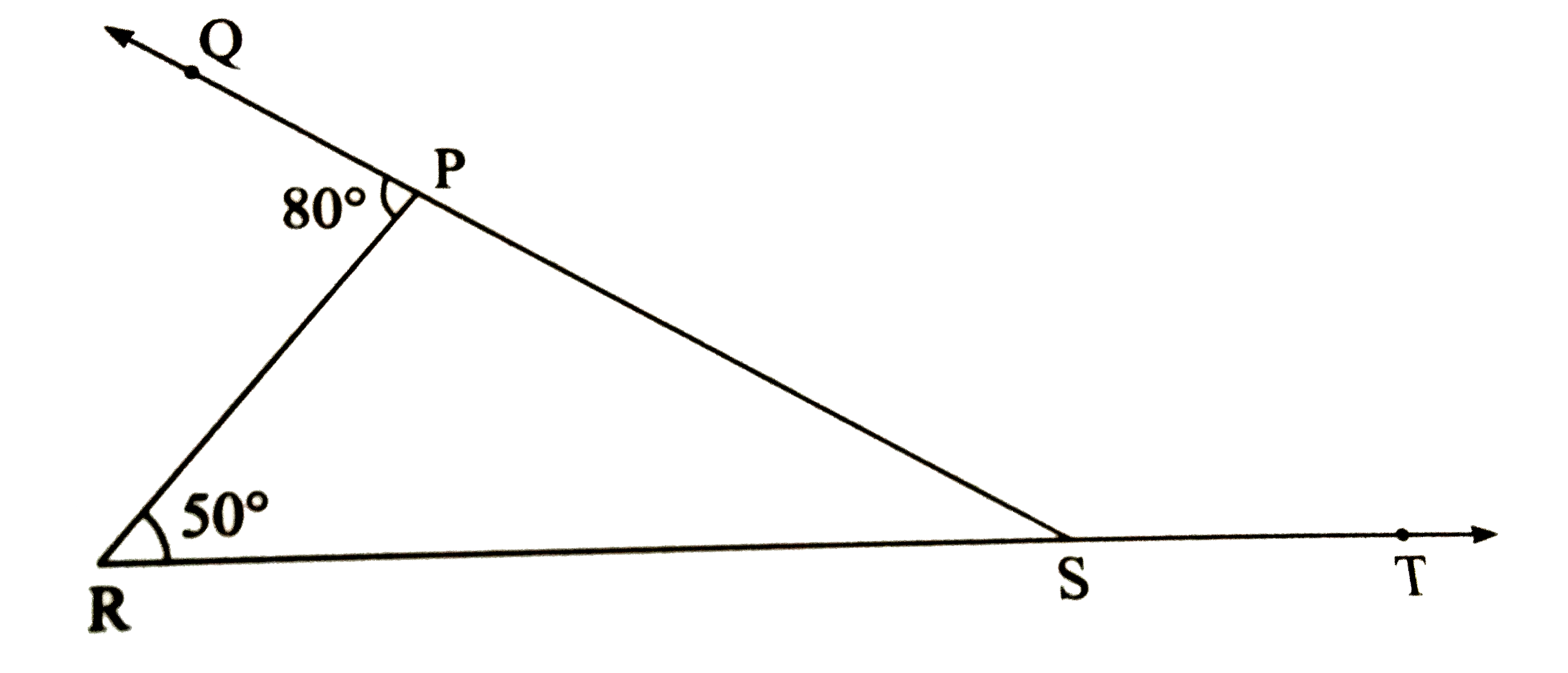
In the figure , ∠ QPR and ∠ PST are exterior angles of △ PRS . If ∠PRS=50∘ and ∠QPR=80∘ , then find measure of ∠ PST.
View SolutionIn a triangle PQR,∠PQR=90∘,PQ=10cmandPR=26cm, then what is the value (in cm) of inradius of incircle?
View Solution
In the figure, PQ=QR,∠RPQ=60∘,and∠QRS=20∘. Find the measure of ∠QSR.
View SolutionIn ΔPQT,PQ=PT. The points R and S are on QT such that PR = PS. If ∠PTS=62∘and∠RPS=34∘, then measure of ∠QPR is
View Solution
