In the adjoining figure, chords AC and BD of a circle with centre O, intersect at right angles at E. If ∠OAB=25∘, calculate ∠EBC

Video Solution
Text Solution
The correct Answer is:∠EBC=25∘
OA=OB⇒∠OBA=∠OAB=25∘
∴∠OAB+∠OBA+∠AOB=180∘⇒∠AOB=130∘
∴∠ADB=12∠AOB=65∘⇒∠ECB=65∘[∠s in the same segement].
Now, ∠EBC+∠BEC+∠ECB=180∘
⇒∠EBC+90∘+65∘=180∘⇒∠EBC=25∘
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12C
26 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
Chords AC and BD of a circle with . centre O intersect at right angles at E. If ∠OAB=25∘, then the value of ∠EBCis
A30∘B25∘C20∘D15∘In the adjoining figure, if chords AB and CD of the circle intesect each other at right angles, then find the value of x+y.
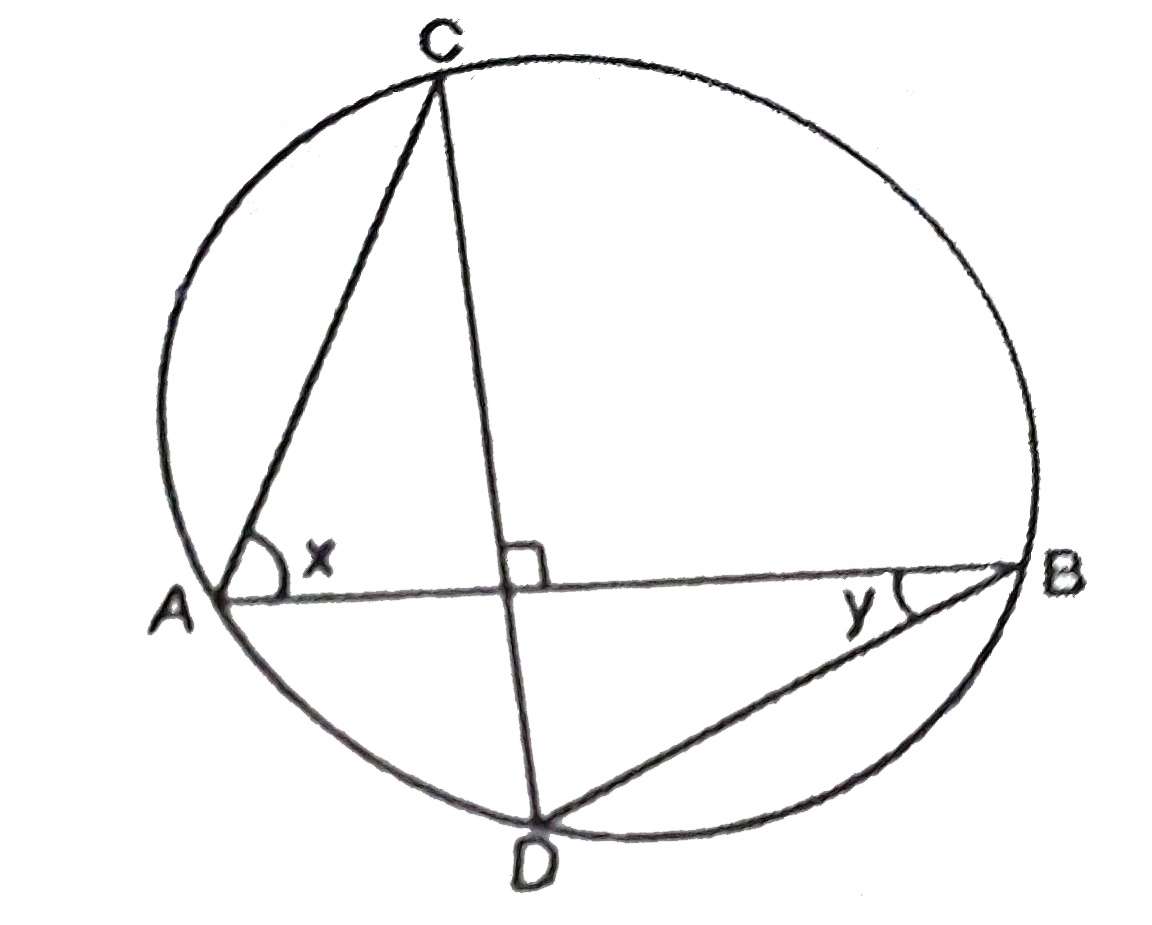 A45∘B90∘C120∘D100∘
A45∘B90∘C120∘D100∘In the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
A36∘B18∘C27∘D36∘
In the given figure, two chords AC and BD of a circle intersect at E.If arcAB=arcCD, prove that : BE=EC and AE=ED
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
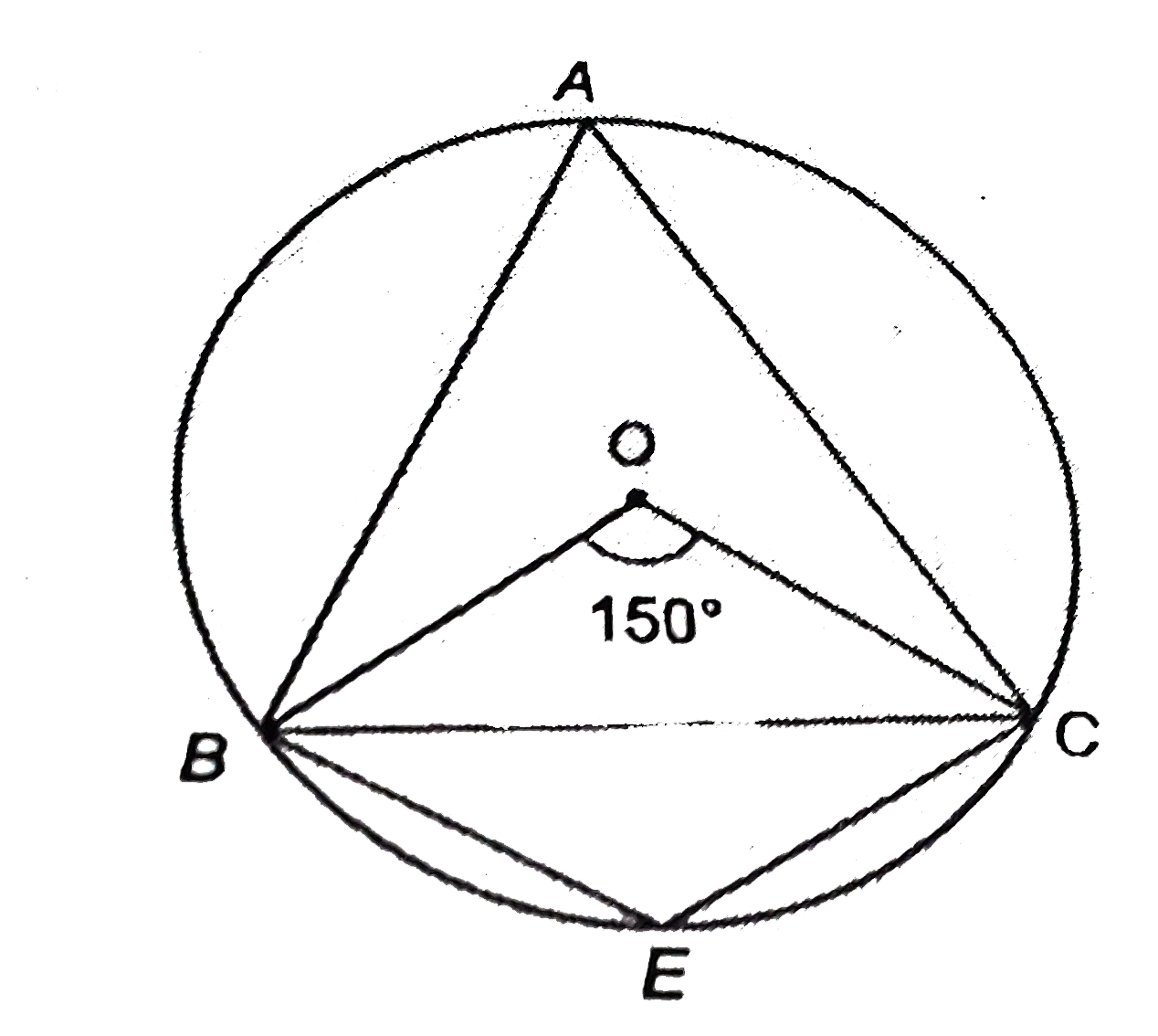
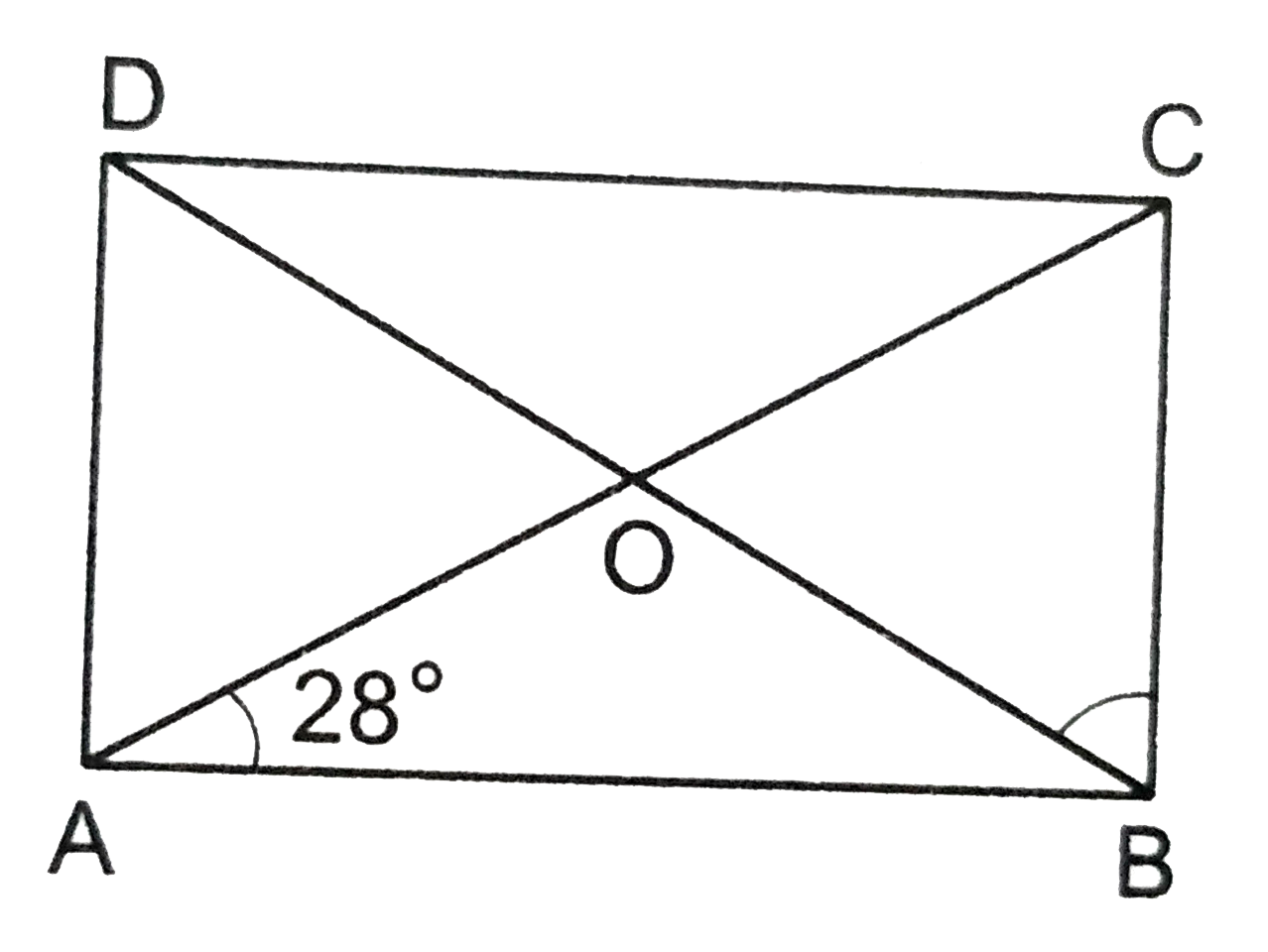
View SolutionIn the adjoining figure, ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB=28∘, find ∠OBC.
View SolutionIn the adjoining figure, DE is a chord parallel to diameter AC to the circle with centre. O if ∠CBD=60∘. Calculate ∠CDE.

View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)

View Solution
