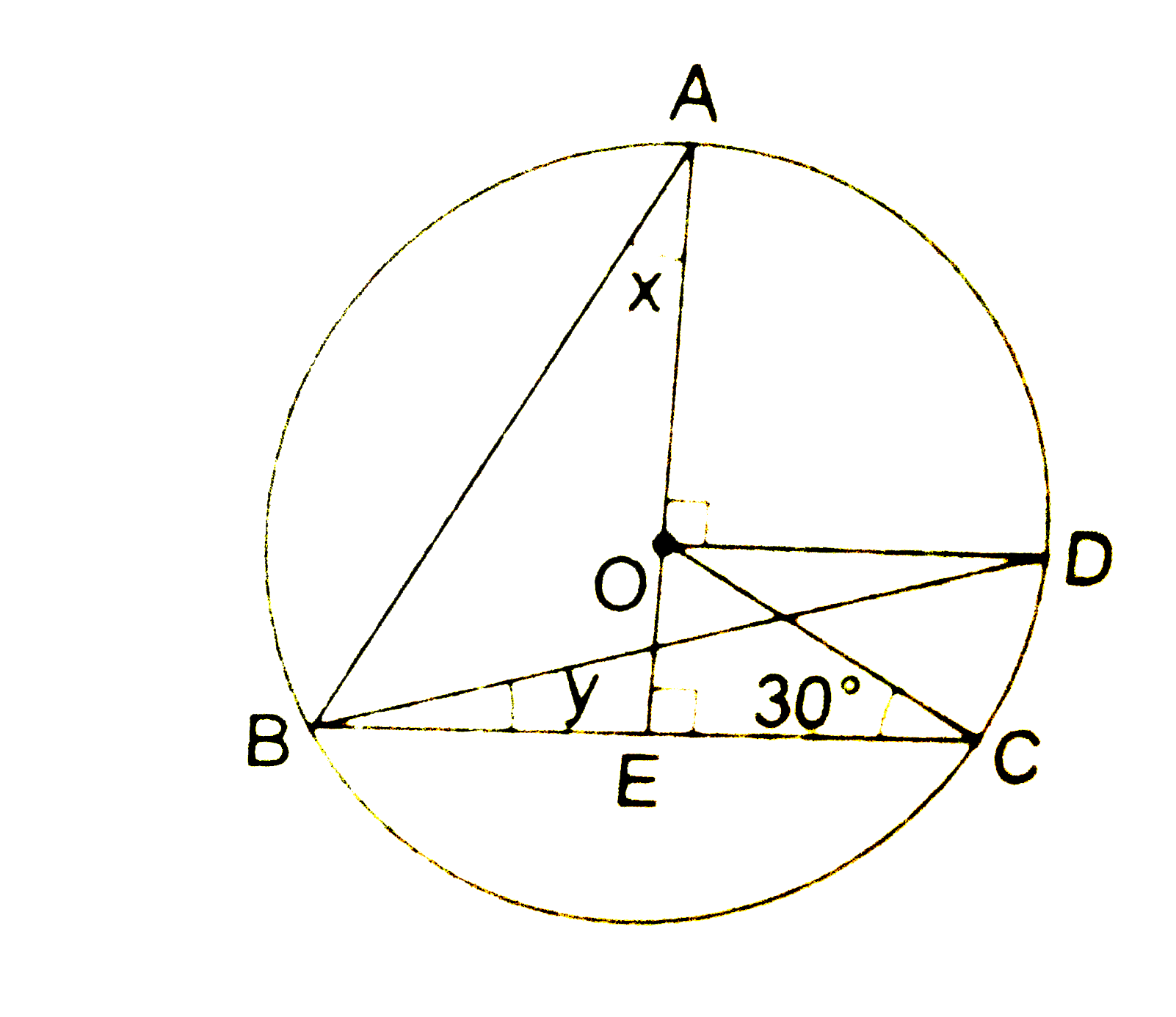
In the given figure, O is the centre of the circle and ∠BCO=30∘. Find x and y .
Video Solution
Text Solution
The correct Answer is:x=30∘,y=15∘
∠AOD=∠OEC=90∘ ( given )
But, these are corresponding ∠s
∴OD∣∣BC.
Now, OD∣∣BC and OC is the transversal .
∴∠DOC=∠BCO=30∘
∴∠DBC=12∠DOC=15∘⇒y=15∘
∠AOD=90∘ ( given )
Now, ∠ABD=12∠AOD=(12×90∘)=45∘
In ΔABE, we have
∠ABE=(∠ABD+∠DBC)=(45∘+15∘)=60∘,∠AEB=90∘
∴∠BAE=180∘−(90∘+60∘)=30∘⇒x=30∘
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12C
26 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In Fig, O is the center of the circle. Find the angle of △ABC.
 A130∘B150∘C135∘Dcan't be determined
A130∘B150∘C135∘Dcan't be determinedIn the given figure, O is the centre of the circle and ∠ACB=25∘ Find ∠AOB
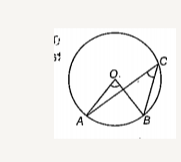 A25∘B50∘C75∘D60∘
A25∘B50∘C75∘D60∘In the given figure, O is the centre of the circle. ∠AOB=70∘, find ∠OCD :
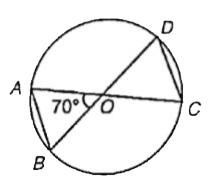 A70∘B55∘C65∘D110∘
A70∘B55∘C65∘D110∘
In figure, O is the centre of the circle ∠BCO=30∘ . Find X and Y.
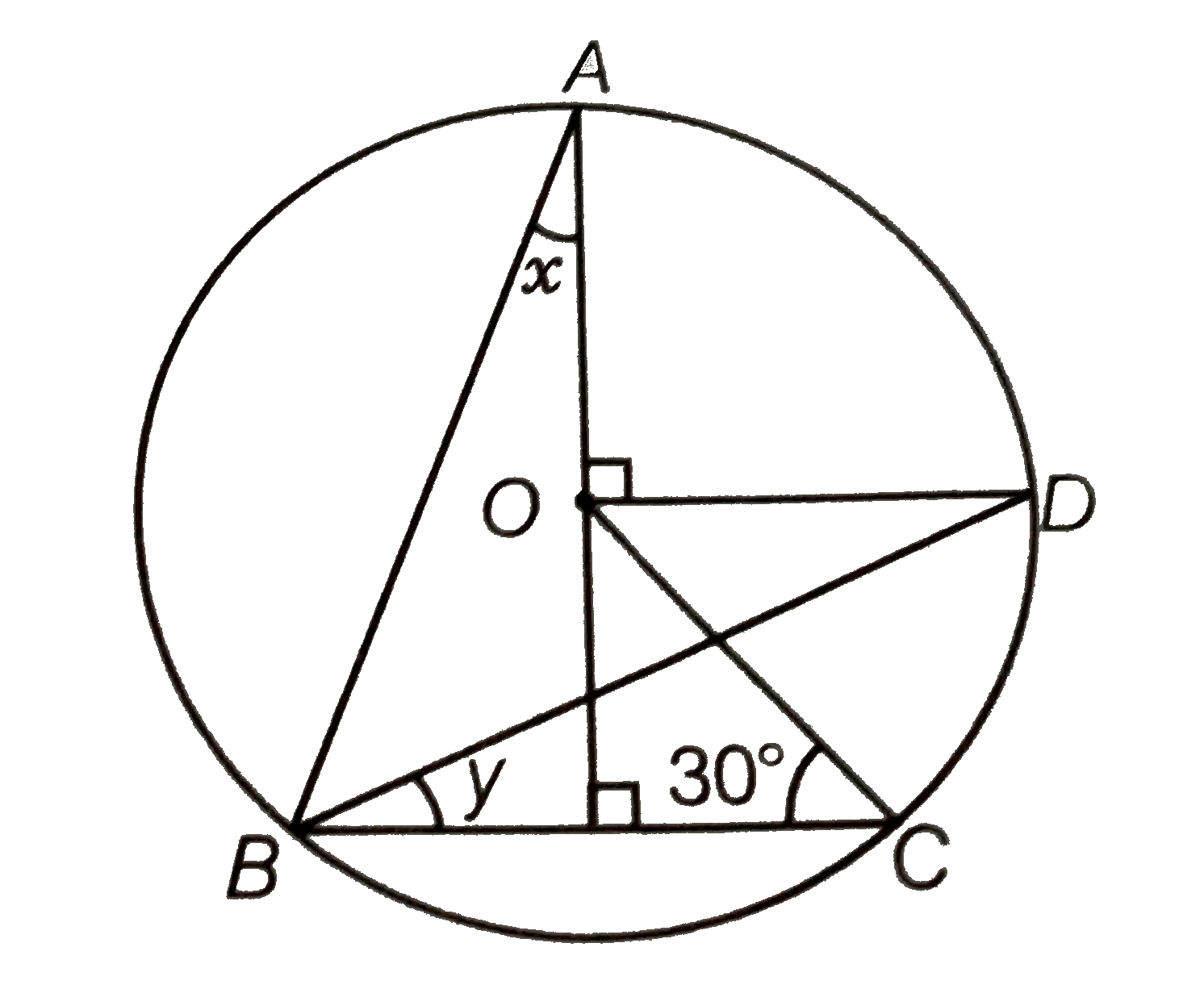
View SolutionIn Figure, O is the centre of the circle. Find ∠CBD
View SolutionO is the centre of the circle ∠BCO=30∘ then find x and y
View SolutionIn the given figure, O is the centre of the circle and ∠AOC=100∘. Find the ratio of ∠ADC:∠ABC :

View SolutionIn the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
View Solution
