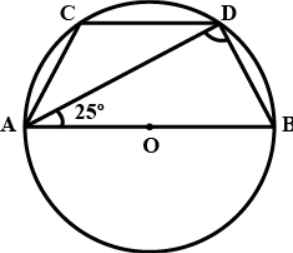
In the given figure, AB is a diameter of the circle and CD∣∣AB. If ∠DAB=25∘, calculate
(i)∠ACD and ∠CAD
Video Solution
Text Solution
Join AC and BD.
We know that an angle in a semicircle is 90∘.
∴∠ADB=90∘
Also, the sum of the angles of a triangle is 180∘
∴in Δ ABD , we have ∠BAD+∠ADB+∠ABD=180∘
⇒25∘+90∘+∠ABC=180∘
⇒∠ABD=180∘−115∘=65∘
Since ABDC is a cyclic quadrilateral, wehave
∠ABD+∠ACD=180∘⇒∠ACD=180∘−∠ABD
⇒∠ACD=180∘−65∘=115∘
Also , AB∣∣CD and AD is a transversal.
∴∠ADC=∠BAD=25∘ [alt. int. ∠s].
Now , in Δ ACD, we have
∠ACD+∠CAD+∠ADC=180∘
⇒115∘+∠CAD+∠25∘=180∘
⇒∠CAD=180∘−140∘=40∘
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD:
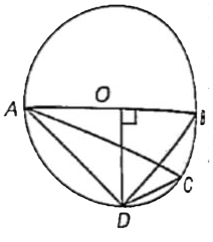 A30∘B60∘C45∘D25∘
A30∘B60∘C45∘D25∘In the given figure, AB is the diameter of the circle, ∠ADC=120∘. Find ∠CAB:
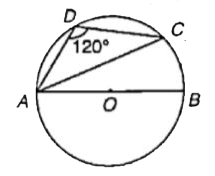 A20∘B30∘C40∘Dcan't be determined
A20∘B30∘C40∘Dcan't be determinedIn the given figure, ∠COB=40∘,AB is the diameter of the circle. Find m∠CAB:
 A40∘B20∘C30∘DNone of these
A40∘B20∘C30∘DNone of these
In the given figure, AB//CD. Find the value of x.
View SolutionIn the given figure O is the centre of the circle and AB||CD. If ∠ADC=25∘, then find ∠AEB∘-

View SolutionIn the given figure, AB∣∣CD. Find the value of x.

View SolutionIn the figure, AB||CD then
View SolutionIn the given figure , AB∣∣CD. Find x.
View Solution

