The bisectors of opposite angles ∠P and ∠R of a cyclic quadrilateral PQRS intersect the correspondig circle at A and B respectively.
Prove that AB is a diameter of the circle.
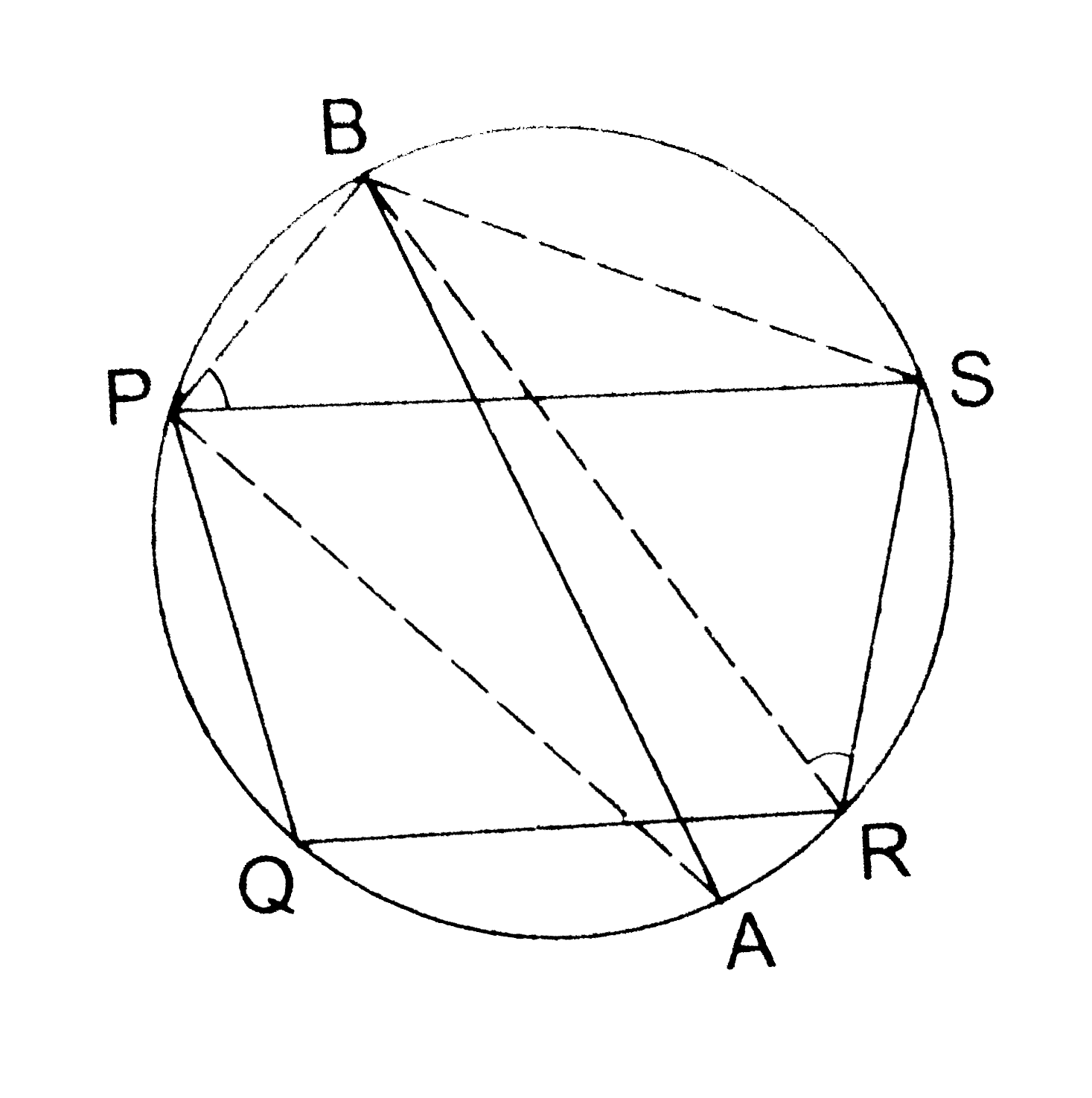
GIVEN A cyclic quad. PQRS in which PA and RB are the bisectors of ∠P and ∠R respectively
TO PROVE AB is a diameter of the circle which passes through the points P,Q,R and S.
CONSTRUCTION Join PB and BS.
PROOF SincePQRS is a cyclic quadrilateral , we have
∠QPS+∠QRS=180∘
⇒12∠QPS+12∠QRS=90∘
⇒∠APS+∠BRS=90∘
⇒∠APS+∠BPS=90∘
[∵∠BRS=∠BPS,∠s in the same segment ]
⇒∠APB=90∘ [∵∠APS+∠BPS⇒APB]
⇒∠APB is in a semicircle
⇒ AB is a diameter of the circle which passes through the points P,Q,R and S
Hence, AB isa diameter of the circle.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A22videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B18videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B16videos
BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
Similar Questions
If the bisectors of the opposite angles ∠Pand∠R of a cyclic quadrilateral PQRS intersect the corresponding cicle at AandB respectively, then AB is a diameter of the circle.
View SolutionIf the bisectors of the opposite angle ∠Pand∠R of a Cyclic quadrilateral PQRS intersect the corresponding circle at A and B respectively; then AB is a diameter of the circle.
View Solution
Knowledge Check
- Question 1 - Select One
PQRs is a cyclic quadrilateral. Find the measure of ∠Pand∠Q.
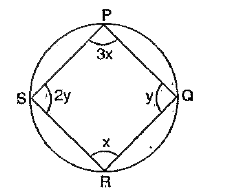 A135∘,60∘B60∘,120∘C60∘,90∘D100∘,120∘
A135∘,60∘B60∘,120∘C60∘,90∘D100∘,120∘ - Question 2 - Select One
In cyclic quadrilateral PQRS, 7∠P=2∠R Then,∠P=
A20∘B40∘C140∘D100∘
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
View SolutionProve that the sum of opposite pair of angles of a cyclic quadrilateral is 180∘
View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices ofthe quadrilateral, prove that it is a rectangle
View SolutionTwo circle intersect in AandBandACandAD are respectively the diameters of the circles. Prove that C,B,D are collinear.
View SolutionIf the diagonals of a cyclic quadrilateral intersect at the centre of a circle , then the quadrilateral is _______________.
View Solution

