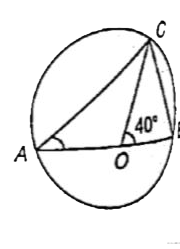
In the given figure, AB is a diameter of the circle with centre O, AC and BD produced meet at E and ∠COD=40∘ . Calculate ∠CED.

Video Solution
Text Solution
Since ACE is a straight line, we have
∠ACB+∠BCE=180∘
⇒90∘+∠BCE=180∘
[∵∠ACB is in a semicircle ]
⇒∠BCE=90∘
Alao, ∠DBC=12∠COD=(12×40∘)=20∘
[ angle at centre =2× angle at a point on a circle ]
⇒∠EBC+∠BCE+∠CEB=180∘
⇒20∘+90∘+∠CED=180∘ [∵∠CEB=∠CED]
⇒∠CED=180∘−110∘=70∘
Hence, ∠CED=70∘
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, AC is the diameter of the circle with centre O. Chord BD is perpendicular to AC. Express p in terms of x.
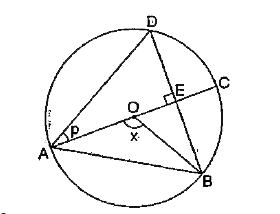 Ax/2B90∘+x/2C90∘−x/2D180∘−x
Ax/2B90∘+x/2C90∘−x/2D180∘−xIn the given figure, ∠COB=40∘,AB is the diameter of the circle. Find m∠CAB:
 A40∘B20∘C30∘DNone of these
A40∘B20∘C30∘DNone of theseIn the given figure , AB is a tangent to the circle with centre O and ∠BPQ=40∘ . Find PQ : AQ.
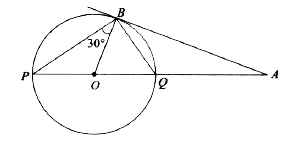 A1:2B1:3C2:1D3:1
A1:2B1:3C2:1D3:1
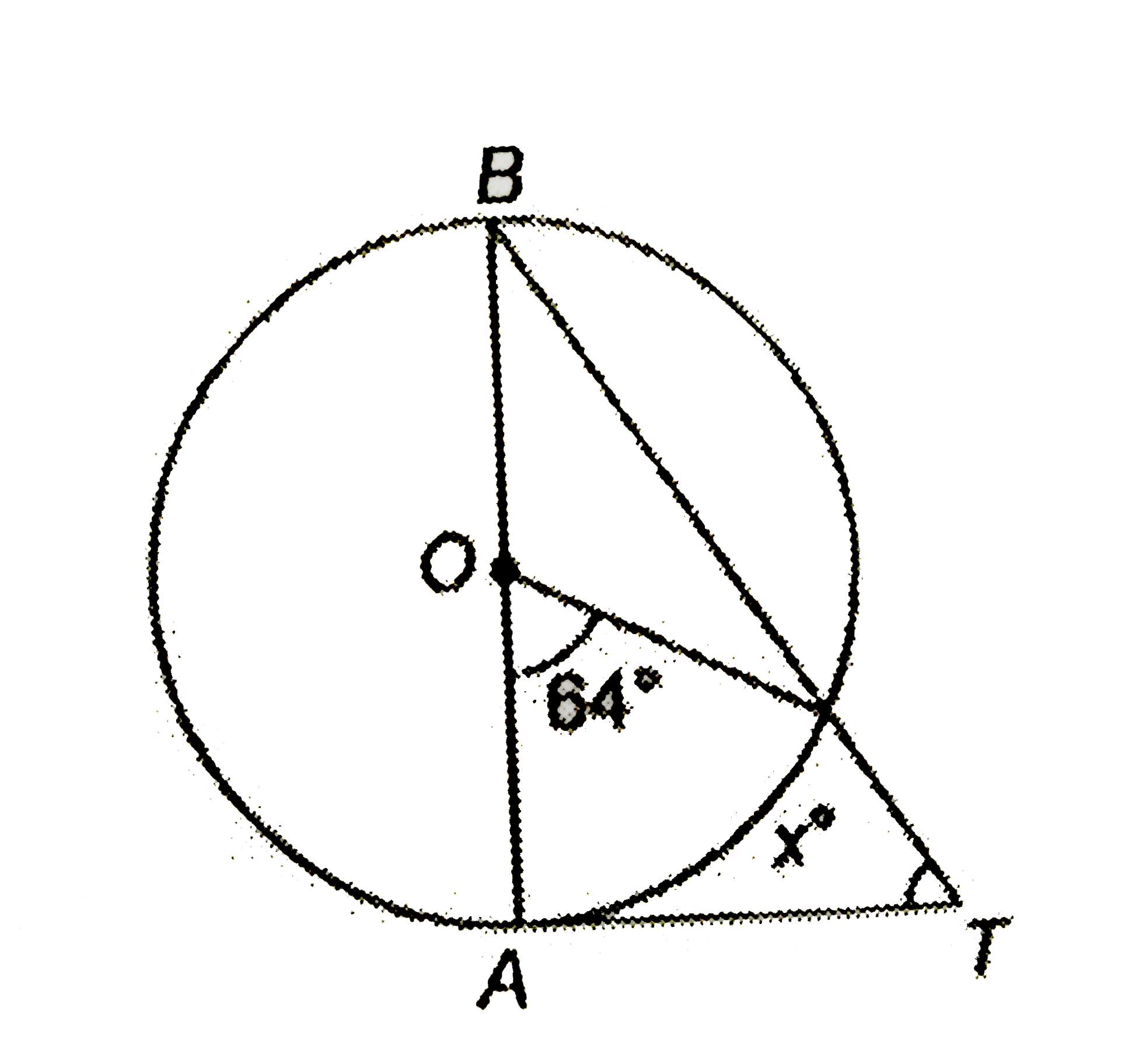
In the given figure, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ=58∘, find ∠ATQ.
View SolutionIn the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
View SolutionIn the given figure, AB is a diameter of a circle with centre O .If ADE and CBE are straight lines, meeting at E such that ∠BAD=35∘ and ∠BED=25∘ find ∠BDC (in degrees)
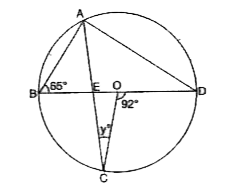
View SolutionIn the given figure, BOD is the diameter of the circle with centre O. ∠COD=92∘and∠ABD=65∘. Then y equals
View SolutionIn the given figure, ∠COB=40∘, AB is the diameter of the circle. Find ∠CAB :
View Solution