In the given figure, O is the centre of a circle . Prove that
∠x+∠y=∠z.
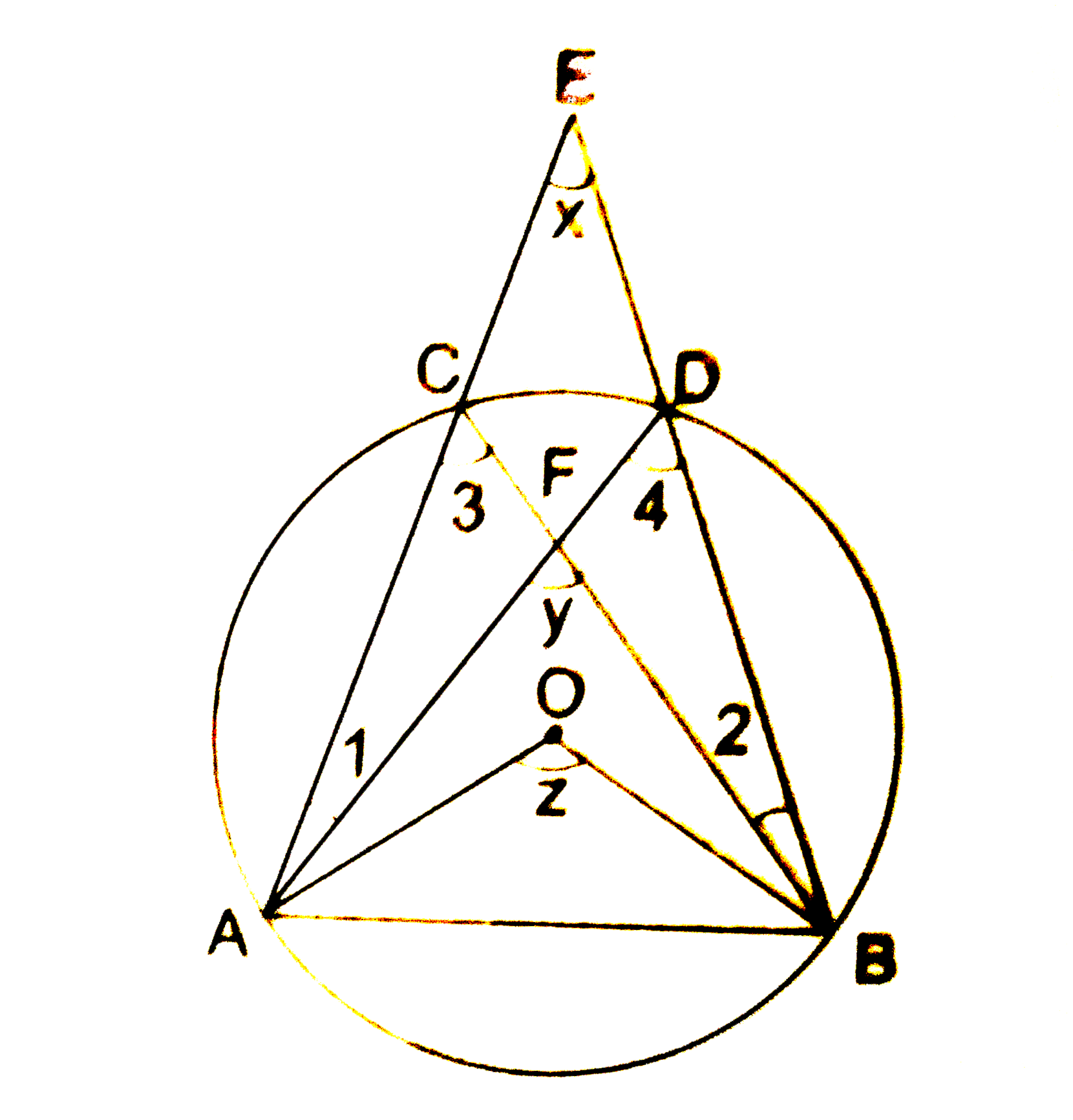
Video Solution
Text Solution
In ΔACF, side CF is produced to B.
∴∠y=∠1+∠3 [ ext. ∠= sum of int. opp. Δs ] …..(i)
In ΔAED, side ED is produced to B.
∴∠1+∠x=∠4 ….(ii)
From (i) and(ii) , we have
∠1+∠x+∠y=∠1+∠3+∠4
⇒∠x+∠y=∠3+∠4
=2∠3 [∵∠4=∠3 angles in the same segment ]
=∠z [∵∠AOB=2∠ACB].
Hence, ∠x+∠y=∠z.
|
Topper's Solved these Questions
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:Exercise 12A
Explore 22 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:EXERCISE 12B
Explore 18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBook:RS AGGARWALChapter:BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONExercise:EXERCISE 17B
Explore 16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle. The value of x is
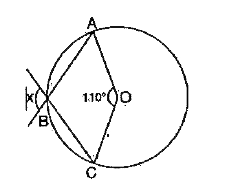 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘In the given figure, O is the centre of the circle. Then ∠AED measure
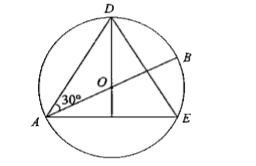 A30∘B45∘C60∘D90∘
A30∘B45∘C60∘D90∘In the given figures, value of y (O is the centre of the circle) is
 A100∘B120∘C130∘D140∘
A100∘B120∘C130∘D140∘
In the figure, O is the centre of the circle. Prove ∠AOC=∠AFC+∠AEC.
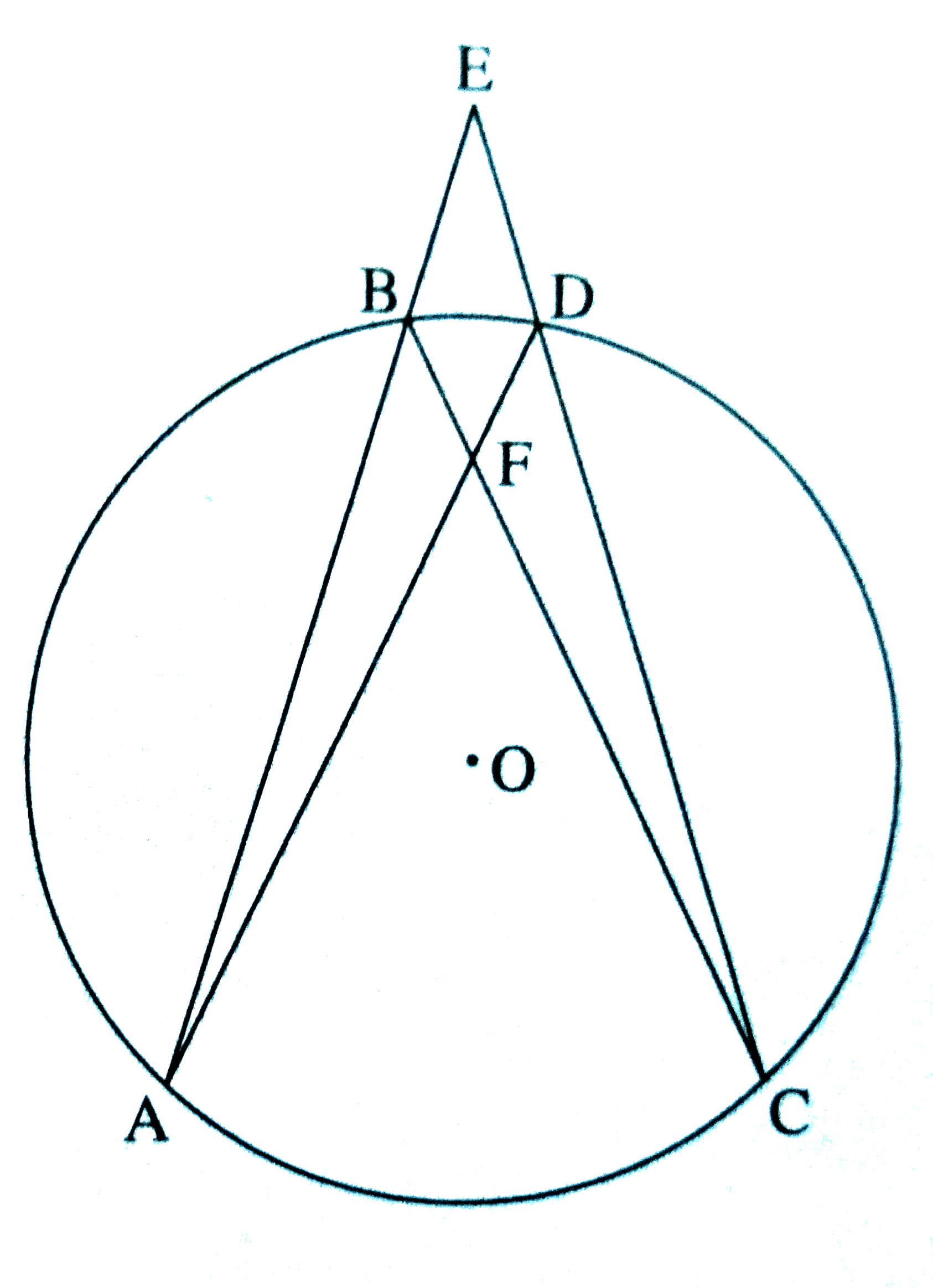
View SolutionIn Figure, O is the centre of the circle. Find ∠BAC
View SolutionIn Figure, O is the centre of the circle. Find ∠CBD
View SolutionIn the given figure (if O is the centre of circle.) , ∠COE measure
View SolutionIn the given figure, , O is the centre of a circle and ∠AOB=140∘. Then , ∠ACB=?

View Solution